I've decided to take a test to past this one. Have been studying during the Summer.
10/04/2014 Update: I got cold feet. So I am taking the class instead. Changing the terms of the topic from Exemption Test to Class.
12/08/2014 Cheikhna Mahawa is the instructor. Very cool, funny one. A quick search showed that he was tortured back home for supporting education for the poor and had obtained asylum here in the States. His interest in teaching and the subject makes him a rare teacher. The only problem is there's no office hour and not enough time to discuss the subject more.
Textbook used: Essential Calculus Early Transcendentals 1st Ed. & 2nd Ed. by James Stewart.

On Vectors
Sir William Rowan Hamilton was indeed a genius. Not only did he invented the cross product, quaternions (precursor of vectors), he could read Latin, Greek and Hebrew at age 5. French and Italian at 8, Arabic and Sanskrit at 10. Later at 21, he was appointed professor of astronomy.
Formulas to Remember:
Vectors:
Terms:
components: the numbers a,b,c inside vector <a,b,c>
position vectors: vectors from point of origin.
standard basis vectors: i, j, k.
Parallelogram
a & b are Orthogonal
a & b are parallel
a & b are orthogonal
Properties of Vectors
Parametric equations for line through (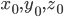 ) in direction of <a,b,c>:
) in direction of <a,b,c>:
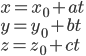
Vector equations for line:
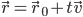
Symmetric equations for line:
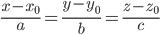
from parametric equations...by defining t...
a,b,c <> 0
Prof. used induction to disprove the Trinity. And here I was beginning to think he was a Christian instead of a Muslim. Because he kept mentioning the Bible and Jesus.
Particularly, he attacked the dual nature of Christ. All focused on the fig tree that Jesus cursed. Mark 11:12-15
To answer is easy, Jesus wasn't omniscient as a man but still God because Prof. missed one important point: Can God not make himself a rock that's so heavy that he couldn't lift himself? Or why wouldn't Jesus be able to have himself not omniscient.
Secondly, I am not sure what Prof. Mahawa was referring to Jesus not being just to the tree that cannot bear its own fruit. We destroy wastes all the time, big deal.
So first error was the assumption of a less capable God, second, it was the false assumption of "innocent" plant. God cursed the earth long ago due to Adam's sin.
Therefore, no induction.
A black lady was rather bothered by it but she was calm. She kept saying Jesus was human, but failed to convince the professor of his proof. I said nothing, because as I predicted, one American white student immediately tried to break the debate and asked for the next lesson. In this secular world, not surprising. And no, I do not think the white guy was Christian by his response, at least not a real one, if any, it would be the inherited Christian type, but I am more inclined to think him a new atheist.
A quick note on Chapter 11.1 Multivariable functions
A function of n variables can be hard to visualize as n gets bigger. But [pg. 622 2nd ed.] provided a good way of seeing it by considering an example of the function as the sum of the total cost of all ingredients purchased where each variable is the unit cost of a unique ingredient.
A quick note on Chapter 11.2 Limits and Continuity
The limit test on multivariable functions that are indeterminate confused me a little. Because I was wondering why not use the epsilon-delta definition to disprove the existence of the limit. The book (page. 627-629 2nd ed.) has only shown how to use the definition to prove that the limit exists as (x,y)-> (a,b), but with functions without such limit, the test is up to intuition.
The reason I failed to understand was a simple one, though I took too long to realize.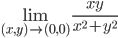
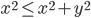 [pg. 629],
[pg. 629], 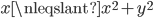 because x could be < 1. Therefore, the journey to build the test by the epsilon-delta def. becomes too tough to handle, the inequality change is causing error in the definition. I noticed the examples given share the same dilemma, so I am unaware if there are different challenges.
Another note is that the inequality sign used in the definition is not
because x could be < 1. Therefore, the journey to build the test by the epsilon-delta def. becomes too tough to handle, the inequality change is causing error in the definition. I noticed the examples given share the same dilemma, so I am unaware if there are different challenges.
Another note is that the inequality sign used in the definition is not 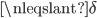 or
or 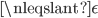 , so that means the test domains and ranges pertaining to the assumed limit L gets smaller and smaller every time.
Others have suggested turning the functions into polar coordinate base.
, so that means the test domains and ranges pertaining to the assumed limit L gets smaller and smaller every time.
Others have suggested turning the functions into polar coordinate base.
For example:
We know that when x=y, limit is different than when x=0 or y=0.
If the test is to be done with the epsilon-delta definition, the we must recognize that unlike Example 4:
A quick note on Chapter 8.3 The Integral Test
2nd ed. pg. 446-447
Why use right end point and the other use left end point of the interval? It has to do with finding the convergence and divergence respectively. Sum of a_n < integral; Sum of integral > a_n.