Prof: Patrick Hooper
http://wphooper.com
Text: LADW (Linear Algebra Done Wrong)
I think they forgot to put the term "Abstract" in the course title.
Linear map 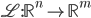 : same as an mxn matrix, A.
: same as an mxn matrix, A.
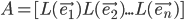 Columns.
Columns.
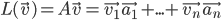
Thus, 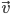 must be in
must be in 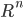 .
.
Prof: Patrick Hooper
http://wphooper.com
Text: LADW (Linear Algebra Done Wrong)
I think they forgot to put the term "Abstract" in the course title.
Linear map 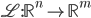 : same as an mxn matrix, A.
: same as an mxn matrix, A.
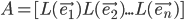 Columns.
Columns.
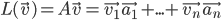
Thus, 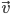 must be in
must be in 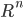 .
.
03/09/2015
Chapter 1, Section 6: Invertible Transformations.
The space of mxn matrices is isomorphic to R^(mn).
If L: V-> W is isomorphism between vector spaces. Then:
1. the entries of V is linearly independent iff entries LV are linearly independent.
Proof discussed.
04/15/2015
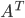 = dim Row A = # of pivots
= dim Row A = # of pivots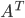
Terms to get:
row A = ran
Rank A = dim Ran A = # of pivots
dim Null A = # of free variables = # of columns without pivots
rank
Thus, rank A = rank
Important note: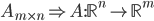
If
4/20/2015
Similar Matrices
Determinant(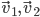 ) is the signed area of the parallelogram P(
) is the signed area of the parallelogram P(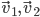 ) with two sides given by the vectors.
) with two sides given by the vectors.
For 2x2 matrix A, Area(A(X)) = c * Area(X)
Area(A(X)) = c * Area(X)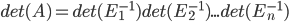
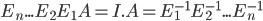
c = |det A|, thus, det A = signed area A(x)/signed Area of X.
So,
If A is invertable, thus,
04/22/2015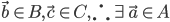 such that i-th column of A =
such that i-th column of A = 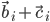 , while the rest of A's columns = B or C's, then det A = det B + det C.
, while the rest of A's columns = B or C's, then det A = det B + det C.
3.3
if
Read Proposition: 3.1, 3.2
04/27/2015
3.5 Cofactor expansion
Theorem 5.1
Reference to sparse matrices for computer science.
Theorem 5.2
Corollary 5.3 Cramer's Rule
04/29/2015
Chapter 2.8
05/06/2015
Chapter 4: Spectral Theory
Eigenvalues, eigenvectors
Diagonalization
05/11/2015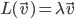
Remarks for Final Exam:
Operator (in differential equations) = transformation = map = function
If L:V->V is a linear transformation, eigen-* involve solutions to
L(f) = f-f'
Eigenvalues and Eigenvectors: Why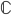
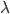 ) is any polynomial of degree n, then p(
) is any polynomial of degree n, then p(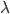 ) has n complex roots counting multiplicity (repeats)
) has n complex roots counting multiplicity (repeats)
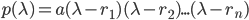
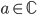
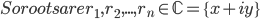
Fundamental Theorem of Algebra
If p(
Complex Conjugation: replace i with -i everywhere. Having a bar on top.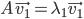
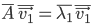
If this is true:
then this is also true:
============================================
Chapter 4.2 Diagonalization.
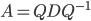
Theorem 2.1, proof.
Theorem: A is Diagonalizable iff for each eigenvalue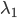 with multiplicity
with multiplicity  , we can find
, we can find  linearly independent eigenvectors.
linearly independent eigenvectors.