Professor Octavio Betancourt
T.A. Mohammed Shibli Saadi
Text: Grimaldi, Ralph P. Discrete and Combinatorial Mathematics, An Applied Introduction, 5th Edition, Addison-Wesley. Downloaded online, free. Looks like the professor had the same version for his projector use.
The syllabus covers only 10 chapters, skipping 8, 9, 14-17.
The text book uses mainly examples to explain, so some ideas are hard to grasp. However, it is thorough enough to learn all kinds of terminologies. One project I could work on is to convert this pdf text to computer readable format as it is now a non-text scan format which makes word search impossible. I shall summarize them here.
The recitation is a joke because the T.A. doesn't really do anything except for telling non-relevant stories and dismisses class early. A time that could have been great for tutoring, even amongst students, without the T.A.
Chapter 1 Principles of Counting
XOR (Exclusive OR)
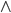AND
1.1
The rules of sum and product:
Condition for Sum:
Condition for Product:
1.2
Permutations Properties:
Distinct = no repetition.
Arrangement: Order is important (relevant).
Arrange = Permute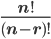
P(n,r) =
However, when arrangements (not permutations) involving indistinguishable (repeated) symbols, the number of arrangements is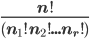
. The denominators pertains to treating the distinct symbols as if they were indistinguishable in order get total count of repeated arrangements.
Arguments that rely on counting: Combinatorial proof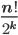
is an integer, where 
:
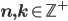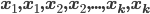. The number of ways in which we can arrange all of these n=2k symbols is an integer that equals 
An interesting trick of proof that
Proof: Consider the n symbols
Circular arrangements involves considering rotation is not important. Thus, we have n!/n.
The challenge of alternating sexes calls for the product rule. Since it is circular and rotation does not matter, one position must be first selected, then label the rest in a diagram and use rule of product to get the answer. [Example 1.17]
1.3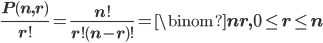
Combinations properties:
Each selection (combination) from n distinct objects, is of size r corresponds to r! permutations, thus, we divide the permutation with r!:
C(n,r) =
It is interesting how C(n,r) relates to Pascal's triangle, which is very useful in finding the coefficients of polynomial equations.
Overcounting is worth noting. pg. 19
Be careful with oversimplifying using only product rule. The rule of product and the rule of sum are used together when order doesn't matter. Generally, this happens in the "at least", "at most" cases, where we may have to add the combinations one by one starting with n, then n+1, etc. when it is "at least n", and so on.
The Binomial Theorem: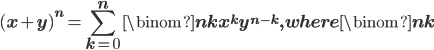
is called binomial coefficient.
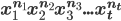in the expansion of 
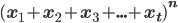is:
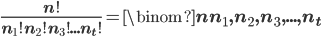where 
we can find the coefficient of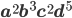 
by determining the coefficient of 
from 
. Thus we can get the term with coefficient from:
.
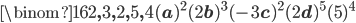From multinomial theorem, we have multinomial coefficient:
The coefficient of
Example: In the expansion of
1.4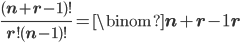
, when we wish to select, with repetition, r of n distinct (but repeating, thus n<r) objects (containers), we find that we are considering all arrangements of r x's and n-1 |'s, in the form of xxx...xxx|||...||| where | is acting as a partition.
Combinations with Repetition
C(n+r-1,r) comes from
Composition: Representations of something where the order of the terms is considered relevant. Example: There are 8 compositions for summands of positive integers totaling 4.
Partition: Representations of something where the order of the terms is considered irrelevant. Example: There are 5 partitions for summands of positive integers totaling 4.
Chapter 3 Set Theory
3.1 Sets & Subsets pg(123[144])
Subset
vs. Proper Subset
vs. <
Just like
For the set of A, the size = cardinality of A, is denoted: |A|
Statements of Proof in Set Theory are called element arguments.
Empty set = null set. Set with 0 element =
= {}.
{
}
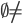Note:
A singleton set is a set with only 1 element. (Unit set)
A power set of A =
in some text is the collection (set) of all subsets of A.
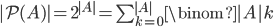
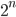? It is ingenious to think of each element as inclusion or exclusion (example 3.7). Thus, the elements can be viewed as a series of binary bits.
Why use
For
I agree with the professor that 0 is not of the element. The text says otherwise.
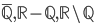, are notations for irrational numbers.
Measure Theory was mentioned. Appears to be a graduate course.
3.2 Set Operations and the Laws of Set Theory pg(136[157])
Union (OR)
Intersection (AND)
Symmetric Difference (XOR)
Definition 3.5 discussed.
Venn Diagram cannot be used as proof. For example: the union of A & B could be represented differently, so the branches of possible paths of proofs could become too complex to contemplate.
S & T are disjoint (mutually disjoint) if S
T = 
Principle of Duality (Definition 3.9 or Theorem 3.5 pg.(141[162])): As per Definition 2.3 or Theorem 2.1 (pg 59[80]). Elaborated in Chapter 15.
Why Venn Diagram is not a valid form of proof: (pg. 144[165]) 1. cannot handle complexity
Example 3.21: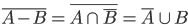
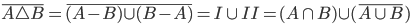Where 
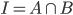and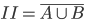 
Gives rise to
3.3 Counting & Venn Diagrams pg. 148 [169]
Chapter 4 Mathematical Induction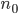
.
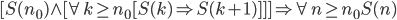
4.1 Well-Ordering Principle
Basic Step: S(1) = true.
Inductive Step: If S(k) = true, then S(k+1) = true.
Proof: Suppose F is a set of natural number, t, such that S(t) is false. F must be empty set. Proof could be done by contradiction (F is not empty).
1 is not necessary the least element. But there must be a least element
Basic Induction:
General/Alternate form Induction: [227]
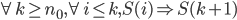
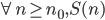
Premises:
i).
ii).
__________________________Conclusion_______
Chapter 5 Relations and Functions
}
5.1 Cartesian Products & Relations [269]
Cartesian product (cross product of sets), e.g. A x B = {(a,b)|
Relation R from A->B is any subset of A x B (binary relation from A to B).
For understanding of Relation and types of functions, see here.
5.2 Functions: Plain and One-to-One [273]
functions are subset of Relation.
f: domain -> codomain.
Range = f(domain) = (subset of codomain).
5.3 Onto Functions: Stirling numbers of the second kind [281]
5.4 (skipped) [288]
5.5 Pigeonhole Principle [294]
5.6 Function Composition and Inverse Functions [299]
Chapter 11 Graph Theory
11.1 Introduction
Definition [535]
Extra: Dense vs. Sparse Graphs (i.e. most edges vs. least edges)
Trail -> Circuit
Path -> Cycle
11.2 Subgraphs, Complements and Graph Isomorphisms [542]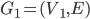
of G has same vertices as G.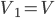 
Number of edges in complete graph:
a_(n+1) = a_n + n
C(n,2) = n(n-1)/2
Spanning subgraph
to be continue...
Isomorphic graph
11.3 Vertex Degree: Euler Trails and Circuits [551]
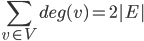for undirected graphs.
Regular Graph: where each vertex has the same k degree. Thus, k-regular graph.
Chapter 12 Trees [602]
12.1 Definitions, Properties, and Examples
G=(V,E) is tree, or = T, if it is connected and contains no cycles.
Forest: More than 1 tree.
From spanning graph we have spanning tree, spanning forest.
Theorem 12:3 In every T=(V,E), |V| = |E| + 1
12.2 Rooted Trees
Only for directed trees.
Rooted tree: Only one root (r). In degree of r = id(r) = 0. All other vertices v has id(v) = 1.
Leaf = terminal vertex = vertex of a rooted tree with out degree = 0.
A vertex in a rooted tree is either a terminal vertex or internal vertex = branch node.
Complete m-ary tree: each internal vertex has exactly m children.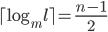
Balanced complete m-ary tree: height =
12.3 Trees and Sorting
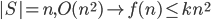
LEMMA 12.1
12.4 Weighted Trees and Prefix Codes
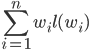
Example 12.17
Lemma 12.2 [633]
Theorem 12.8 [634]
I am sure you did not make good grade. That's why felt that way
Ya I got a G
See I am right....Those people talk too.. they can't do any thing like you. When some one criticize to other means he himself has the problem.
timlyg, you are sick. You spent so much to do this. You could have done better more study with other.
What I don't get is that why the joker(s) above seem to think I have a problem/beef with this class.
No matter other students say, I like most of this class and love to take another class if he class.
You love the class? So do I!!!
He is the great teacher I had even bin.