Instructor: Gennady Yassiyevich
Science: Inductive, Empirical, Scientific Method
Math: Deductive, Rational, Axiomatic Method
Natural numbers defined elegently by empty sets?
0 is in N here.
=========
Logic:
Statement (able to assign truth value) or closed sentence vs. open sentence: P(x)
# arithmetic mean >= geometric mean
Universal statement, existential statement, Converse.
# P=>Q equivalent -P v Q

02/05/2015
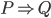 is the converse of
is the converse of 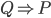

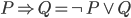
Recaps involving LateX syntax (Chart recommended by Prof.):
Notations:
Recall from CSC10400:
In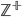 : Prime numbers are the opposite of composite numbers.
: Prime numbers are the opposite of composite numbers.
Tautology vs. contradiction
02/10/2015
Lecture 4
Vacuous Proof: When hypothesis is false -> Conditional statement is vacuously true.
"IF" in Definition: ... if ...., is always = iff = if and only if (both directions).
02/17/2015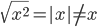
Lecture 5
Terms:
- Parity: The state of being either even or odd. (e.g. 3 has parity odd)
- "Without loss of generality"
- In Definitions, the "if" always means "iff" (if and only if)
- A ≡ B (mod C): A is congruent to B modulo C, invented by Gauss.
-
02/19/2015
Lecture 6
Proof by Contradiction. "Reductio ad absurdum"
Q.E.A. (ancient notation like Q.E.D.)
off topic:
pi is irrational (proven by Lambat in 1777)
e is irrational (Euler/Fourier proved it)
pi + e is irrational? unsolved.
Theorem (Pythagoras):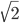 is irrational
is irrational
Fundamental Theorem of Arithmetic
02/24/2015
There are Constructive & non-Constructive proofs. The latter one is also called existence proof or existence theorem: proving without providing an example.
There is an interesting example for the existence proof: which is the irrational set, such that
which is the irrational set, such that 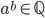 , which is rational.
, which is rational.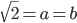 . Thus we have
. Thus we have 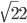 . So here
. So here 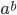 can either be rational or irrational. If it is rational, then the case is solved. If it is irrational, then we have a new set of irrational numbers such that
can either be rational or irrational. If it is rational, then the case is solved. If it is irrational, then we have a new set of irrational numbers such that 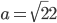 and
and 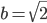 . Now,
. Now, 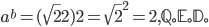
Proposition:
Proof: Take irrational number
The constructive proof for the same example is also interesting, check link.
Lecture 7. Generalized principle of mathematical induction.
02/26/2015
Lecture 8. Strong Induction Principle & well-ordered sets.
notes: (0,1) = ]0,1[ <== French notation (rarely used) Empty set is well-ordered because empty set is true vacuous.
03/03/2015
Lecture 9. Conjectures in Number Theory ("Arithmetic" is the term preferred by Prof.)
Number Theory: Math subject which studies the integers.
Conjecture examples:
1. Diophantine equations: x^2+y^2=z^2 (Prof: solutions in textbook), Fermat's last theorem (solved), etc.
2. Prime number distributions: twin prime conjecture (unsolved) - Zhang 2014 solved the weaker version. Bertrand Conjecture: between n & 2n there is a prime (proven about 100 years ago).
3. Additive problem: Goldbach Conjecture. Every even number is a sum of two primes (unsolved). Weak Goldbach: Every odd integer is a sum of 3 primes (proven). Goldbach Conjecture implies Weak Goldbach.
Alexander Grothendieck, good at solving conjectures.
Poincare Conjecture (look up classification of compact complex surface) mentioned in reference to topology (study of space):abstract version of geometry without distance. e.g. sphere, n-torus, Klein bottle, etc. The one who solved it quit math.
Why do these? My answer is that one reason is to refute charlatans who find loop holes in population's weak understanding of math.
Knot theory mentioned. Not knots, etc. Useful now in molecular biology.
Mentioned an insect that survives at 300 & -300 degree.
03/05/2015
From Prof.'s book.pdf
Chapter 1. Equivalence Relations and Partitions
Pairs, relation R, Cartesian product.
relation, aRb: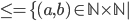 a is not larger than b
a is not larger than b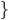 Thus we write "a
Thus we write "a b".
b".
3/10/2015 or A/~ (A modulo the equivalence relation)
or A/~ (A modulo the equivalence relation)
Chapter 1. Sect. 3
Equivalence Classes
Notation: [a] or
03/12/2015
Lecture on partitions.pdf
For congruence modulo equivalence relation, Z/3Z = Z/~ = {[0],[1],[2]}, Notation is Z/nZ. Thus, |Z/nZ| = n.
"/~" is modulo equivalence. Z/~ is set of the equivalence class.
Z is the set of integers.
Group is introduced. e.g. Z/nZ
[1]+[2]=[3]=[0]
[4]+[14]=[18]=[0]
03/17/2015
Functions
"!" means unique in math language. Note in computer language, "!" means differently viz. not
Prof: Fourier accepted his own paper when he became president of the school.
03/19/2015
Study on Composition of functions.
Commutative Ring theory nothing to say to non-commutative ring theory. Very different fields of study.
On compositions of functions being associative, examples of non-associative operations were asked. Prof used power raising (e.g. (3^3)^3 != 3^(3^3)). I believe division "/" is also another example.
03/24/2015
Prof. mentioned Emmy Noether.
Prof: 25-page proof solved by Paul Erdős in 4 lines.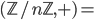 fundamental Abelian group
fundamental Abelian group
Fathers of Group:
Niels Abel - Norway (1802-1829)
Evariste Galois - French (1811-1832) (died young in duel, before recognition by Fourier due to a paper sent to Fourier).
03/31/2015
Set theory - by George Cantor (1845-1918)
Math community not so welcoming it. Poincare called it a disease. They come up with contradictions against set theory.
David Hilbert (1862-1943) supported Cantor.
Graduate set theory: Axiomatic Set Theory
Continuum hypothesis - caused Cantor admitted into mental asylum. Affected Gödel as well. Turing also dealt with this. whether it's related or not, he committed suicide. Hence, prof. said we are threading on dangerous ground.
Chapter 3: Cardinality theory
===============
(The theory of ordinals)~(graduate course).
Transfinite numbers vs. regular numbers.
(Transfinite induction)~extra knowledge.
Proposition, sets A, B, C can be similar to equivalence classes but are not.
Wilson's Theorem: Prime number test. if n|(n!+1), then n is prime.
So example for |A| < |B| for "strictly" smaller. Cantor-Schroeder-Bernstein Theorem: IFF |A|<=|B| and |B|<=|A|, then |A| = |B| Long proof summarized: If there is an injection f:A->B
and another injection g:B->A
Then there exists h:A->B which is a bijection.
Cantor used the theorem to show |Real| = |R^2|
Beyond scope of this class: For any two sets, is it true (Yes) that |A|<=|B| or |B| <= |A|.
04/02/2015
Prof.'s fun note: Killing Form in math, named after a person called Killing, does not mean the verb kill.
04/14/2015
Terms:
Cantor's diagonal argument
Degenerative Interval
Dyadic
Binary Expansion
Next session: Are there any set strictly larger than some uncountable sets.
04/16/2015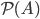 |
Terms: Ordinal
|
Terms: Ordinal
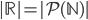
Theorem 2 (Cantor) for any set A, |A| < |
04/21/2015
Proof of Cantor-Schoeder-Bernstein Theorem
Using hand waving proof (meaning using not technical method).
Proposition #13 (pg. 32)
Prop: |Complex| = |Real|, Proof: start with f: RxR -> C, it is understood that f(x,y) = x+iy is bijective. Hence, we know |RxR| = |R| => |R| = |C|.
Proposition #14. Note: A can be either countably infinite or finite set.
Undefined terms: set, element of.
Properties of undefined terms: Axioms.
A set is really just a collection of sets.
e.g. Axiom of existence: There is s set x, so that any set y, such that y is not in x. Basically the definition of an empty set.
Zermelo-Fraenkel - choice set theory Axioms.
Mathematics: It's more important what something does than what something is. Category theories. Focusing more on arrows (properties) than objects (thing in itself).
Feynman on Math
https://www.youtube.com/watch?v=obCjODeoLVw
04/23/2015
Prof: Calculus considered pseudomath since 1600s, until Augustin Cauchy (1789-1857) & Karl Weierstrass (1815-1897) Father of modern analysis. Mathematicians don't say calculus, they say analysis.
Derivative introduced by Fermat.
Probability also was considered pseudomath since 1600s. Recently formalized by Andrey Kolmogorov (1903-1987) in the 1930s.
To test if something is irrational: use Rational Root Theorem
4-color problem was unsolved for a long time until they had a computational proof that it is possible, but it was so computational that they use computer to show it.
Proof of Transcendental number exists (proven by Cantor, but no one could give an example). Example: Liouville's Number.
Proof is in book: Measure & Category by Oxtoby.
more examples of transcendental numbers: e, pi (lindemann weierstrass theorem)
Constructible vs. non-constructible number (Euclid)
For ridiculous math solutions from math students: http://mathoverflow.net/
04/28/2015
In the book, Dedekind cut: Definition of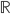 .
.
Chapter 3. Completeness
3.1 Bounded sets
The upper bound (only one) vs. "an" upper bound.
Empty set is bounded by any real number. <= Vacuously true. Notation: (0,1), some preferred ]0,1[ in order to avoid confusion with an ordered pair, but it is not popularly used. sup(A) not necessarily = max(A). Same thing with inf(A) and min(A). Completeness property: key to Real Analysis.
04/30/2015
Archimedean Property.
Zorn's lemma mentioned. To show that not all lemmas are trivial.
Lemma 7.
Possible Final Exam question: a is in A)
Supposed A is countable set of real numbers. Prove that R\A is dense.
Proof: Suppose R\A is not dense. There exist x, y with x
But then |(x,y)| leq |A|. But |(x,y)| = |R| and |A| = |N|, thus this is impossible. Q.E.D.
05/05/2015
Limit of sequence defined by Karl Weierstrass. Convergence of sequences: most important definition in advanced calculus.
Proof of convergence, possibly on Final.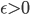 , choose N = ...
, choose N = ...
First lines: Let
From previous session: Triangle inequality, most used in advanced calculus. |x| + |y|
|x| + |y|
|x+y|
Check yellow analysis book for more examples.
05/07/2015
Bounded Sequences: Proposition 2 & Proof
Monotone Sequences
Prof: Manifold with boundary is also manifold without boundary.
Bounded Monotone Convergence Theorem
Theorem 1. If a is both bounded and monotone then it is convergent. Proof.
series 1/n^2, Euler showed it converges to (Pi^2)/6. Euler became blind later in life and solved the 3-body problem.
05/12/2015 } we say C is nested, such that if
} we say C is nested, such that if 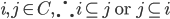 .
.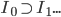 , C = {I_0,I_1,I_2,...} is nested.
, C = {I_0,I_1,I_2,...} is nested.
Another way to prove uncountable Real, other than Cantor's.
Theorem (Nested interval):
Def: Let C be a collection of closed invervals, C = {[-n,n]: n
Now, we construct
The theorem: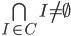 .
.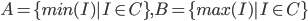
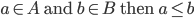 .
.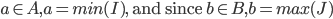
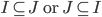 .
.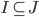 then,
then,
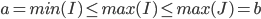
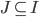 then,
then,
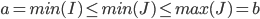
Let C be a (non-empty) collection of closed intervals. Then
(More simply, there exists a number p, so that p is in I, for any I in C)
Proof: Let
We claim that if
Since
But C is nested, so either
i). If
ii) If
This justifies the claim.
Choose any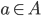 , for any
, for any 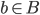 , we have
, we have 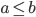 .
.
Thus a is a lower bound for B.
Hence,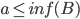 = greatest lower bound for B.
= greatest lower bound for B.
This inequality is true for any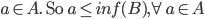 .
.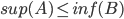 .
.
Therefore, inf(B) is an upper bound for A. Thus,
Pick any number p, so that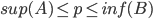 ,
,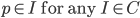 .
.
It remains to show that
If , then
, then 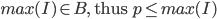 .
.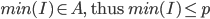 .
.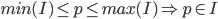 (I is closed).
(I is closed).

And, since
In particular,
Hence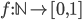 , there exist
, there exist 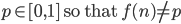 .
.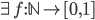 bijection.
bijection.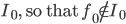 .
.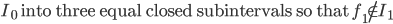 .
.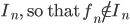 .
.
Prop: If
(i.e. thesequence f_0, f_1, ... does not contain every number in [0,1].
Cor: [0,1] is uncountable.
Proof:
(If countable, then
But by prop, there is no surjective function.)
Divide [0,1] into three equal closed subintervals, choose the subinterval, call it,
Subdivide
Keep on doing this, construct
Since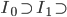 ...
...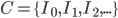 , then C is nested collection of closed intervals.
, then C is nested collection of closed intervals.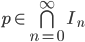 . (p is contained in every
. (p is contained in every 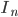 ).
).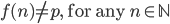 .
.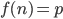 for some n, then
for some n, then 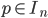 but
but 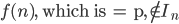 ,
,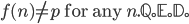
If we let
By the theorem, there exist
We claim that
Suppose not, if
This is a contradiction,
From book Measure and Category - Oxtoby. [pg 1?]
Measure is about the length of a set. Category (outdated term) is about the density of a set.
Cantor set (removing all middle thirds, length of zero, but...) <= notion of fractal, repeated pattern.