By Prof. Vladimir Shpilrain
He walks out of class faster than we can say "Do we have syllabus?"
Text: Kenneth Rosen's Discrete Mathematics and Applications
Operations on sets:
Symmetric difference of A and B: 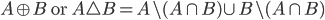
Non-deterministic infinite sequence: e.g. coin tosses.
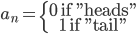
Th, 9/10 - no class (M schedule)
Tu, 9/15 - no class (holiday)
Th, 9/17 - no class (Prof. out)
Tu, 9/22 - no class (holiday)
----------------------------
Th, 9/24 - yes
F, 9/25 - yes (T schedule)

09/01/2015
HW assignments Chapter 2
p. 125, Ex. 9, 21, 22, 30
p. 136, Ex. 15, 29, 30
p. 168, Ex. 9, 12, 18, 29, 32
Chapter 5 Mathematical induction
1. base induction: prove P(1) is true.
2. STEP of induction: prove if P(k) is true, then P(k+1) is true.
Strong mathematical induction: similar, but step 2 is as follows:
2. prove that if P(1), P(2), ..., P(k) are true, then P(k+1) is true.
09/03/2015
Chapter 6: Counting
Questions are found in text book.
Number of functions (F: X_m-> Y_n) frm domain of cardinality m to codomain of cardinality n = n^m
Can be view as base of n, with length of m. Such as when dealing with power set of a set A => P(A) = 2^|A|
How many One-to-one functions from X_m -> Y_n? restriction (m <= n). Thus, n(n-1)(n-2)...(n-m+1), why +1 in the end? because (n-0) was the first term, hence, without -m+1, there will be m+1 terms, but we want m terms only.
How many bit strings of length 7 either begin with two 0s or end with three 1s?
| A U B | = |A| + |B| - |A n B|
A: bit strings that begin with two 0s = |A|=2^5
B: bit strings that end with three 1s = |B|=2^4
|A n B| = 2^2
thus, total = 44.
The Pigeonhole principle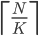 objects.
objects.
The generalized pigeonhole principle: If k+1 or more objects are placed into k boxes, then at least one box will contain at least 2 objects.
If N objects are placed into K boxes, then at least one box will contain at least
09/08/2015
HW#2.3
p.329: Ex. 5, 6, 15, 20,21,28,31,32,33,49
p.396: Ex. 7,11,16,27,29,36,44,47,50
p.405: Ex. 3,9,12,14,35
6.3 Permutations:
A permutation of a set of distinct objects is an ordered arrangement of these objects.
A one-to-one function.
p(n,r)
Combinations
An r-combination of a set of distinct elements is an unordered selection of r elements of this set.
C(n,r), divide by r!, because we count unordered arrangement now.
Ex. A coin is flipped 10 times, how many outcomes are there in total? 2^10
a) If we are only interested in the number of "heads", then the answer is 11.
b) how many possible (ordered) outcomes contain exactly 3 heads? C(10,3).
c) how many outcomes contain at least 3 heads? C(10,3), C(10,4), ... C(10,10) = 2^10-(C(10,2)+C(10,1)+C(10,0)) = 968
d) how many outcomes contain the same number of heads and tails? C(10,5)
Ex. How many permutations of the letters ABCDEFG (pg. 414, #21, #31)
a). contain the string ABC? 5!
b). contain the string CFGA? 3!
c). contain the string BA and GF? 5!
...
#31. b) 21^4 * 5^2 * C(6,2)
C(6,2) is the # of positions for the 2 vowels.
09/24/2015
HW#4
p.432, Ex. 7,8,11,14,15,17,20,21,23,27,30,32,34,35
6.5
Combinations with Repetitions
The number of ways to distribute n indistinguishable objects into k distinguishable boxes is C(n+k-1,n) = C(n+k-1, k-1)
Shown Ex. 3. (pg 424)
09/25/2015
Test 1 will be Tue 10/6, Sections 6.1,6.2,6.3,6.5
6.5 Permutations with Repetitions
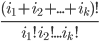
Suppose there are i_n objects of type n
(objects of the same type are indistinguishable)
Then the number of permutations of all these objects is:
Ex. like example 7 pg. 427.
Ex. How many different bitstrings should be formed using 8 zeros and 7 ones?
15!/(8!7!), same as C(15,8)=C(15,7)
Ex. How many ways are there to deal 52 cards to 4 players? (each should get 13 cards)
C(52,13) * C(39,13) * C(26,13)
(Similar to example 8 (pg. 429), but note something different from the book, prof. said the players are indistinguishable while the text labeled distinguishable).
Tough Ex.
A shelf holds 12 books in a row. How many ways are there to choose 5 books so that no two adjacent books are chosen?
Solution:
use "|": books chosen
"*": books not chosen, e.g. *|*|**|*|*|*
6 boxes and 5 objects. Let x_i be the number of objects that go to box number i:
Then: x_1 + x_2 + x_3 + ... x_6 = 7.
x_1, x_6 >= 0, x_2...x_5 >= 1.
answer: (6+3-1,5) = (8,5) = (8,3)
Ex. How many ways are there to distribute 5 distinguishable objects into 3 indistinguishable boxes?
(Example 10, pg. 430)
Prof's method:
1) 5 = 5+0+0
2) 5 = 4+1+0
3) 5 = 3+2+0
4) 5 = 3+1+1
5) 5 = 2+2+1
thus,
1) 3 ways
2) 3 * (2*5) = 30 // choose empty box, choose box with 1 object, objects that can go in that box
3) 3 * (2*(5,2)) = 60
4) 3 * (5,3) * 2 = 60 // 3 is from choose box with 3 objects
5) 3 * 5*(4,2)*2 = 180 // 3 is choose box with 1 object, 5 is choose 1 object for this box.
Total: 3+30+60+60+180 = 333
Then someone mentioned this would solve for "distinguishable boxes". Where he
So, Prof. replace the "3", "2" of each cases with 1. Thus answer becomes 56 instead of 333.
I asked if the previous case was for solving "distinguishable boxes", prof answered no.
??
this is from #50, pg. 434.
Google shows different answer, which like the text book, uses something called the Stirling Number of the Second Kind. S(n,k). Taking the sum S(5,3)+S(5,2)+S(5,1) = 41.
The definition of the S(n,k) is number of distribution of n distinct objects into k indistinct NON-EMPTY boxes. Hence, by doing the sum, we removed the condition of "NON-EMPTY".
The textbook uses a sum function to define S(k,n).
Another definition of S(n,k), using recurrence relations = S(n-1,k-1) + kS(n-1,k)
Prof.'s method seems to be valid except for case 5: (2+2+1). It should have been 3*5 = 15. Which is 5*(4,2)/2.
09/29/2015
Recurrence relations discussed.
Ex. Find a recurrence relationship and initial conditions for the number of bit strings of length n that do not have two consecutive zeros?
Let a_n be the number of bit strings of n length that do not have two consecutive zeros.
1). a_n = a_{n-1} // last bit is 1
2a) a_n = a_{n-2} // last two bits are 10
2b) a_n = 0 // last 2 bits are zeros
Total: a_n = a_{n-1}+a_{n-2}, a_1 = 2, a_2=3
If it has two consecutive zeroes, a_n = a_{n-1}+a_{n-2}+2^(n-2), a_1 = 0, a_2 = 1.
(non-homogeneous mentioned pertaining to this).
Ex. Find recurrence relation for the number of permutations of a set of n elements.
Ans: a_n = n*a_{n-1}, a_1 = 1.
Something about not able to solve for this, due to increment coefficient.
My other notes:
pg. 507.
Catalan numbers is an interesting topic. It as history before Catalan himself, even in China. It's a study of combinatorics in partitions and stuff, Richard P. STanley's book: Enumerative Combinatorics: Vol. 2 as 66 applications for it.
10/01/2015
HW #5
p.510, ex. 7,8(a,b), 9(a,b), 10, 24, 28
p.524, ex. 3(a,c,e), 4(a,b)
8.2 Linear homogeneous recurrence relations with constant coefficients
Definition 1.
Characteristic equation (pg. 515)
General solution = theorem 1.
Example 4 in pg. 517 shown
10/08/2015
HW#6
p.524, Ex. 3(a,c,e), 4(a,b)
p.525, Ex. 7, 12, 20, 22, 26,27,28,29
Test 2: Oct. 29, Sections
8.1,8.2,10.1,10.2,3, 4 (tentatively).8.2: Linear non-homogeneous recurrence relations with constant coefficients
(similar to pg. 521)
(*.)a_n = c_{n-1}a_{n-1}+ c_{n-2}a{n-2}+...+c_{n-k}k(a_{n-k}+F(n)
let a^(h)_n be the general solution of the associated homogeneous relation (ie. with F(n) = 0).
Let a^(p)_n be a particular soltion of the given non-homogeneous relation,
then a_n = a^(h)_n + a^(p)_n
Finding a^(p)_n for F(n) of the form P(n)\times s^n, where P(n) is a polynomial in n.
(1.) S is not a root of the characteristic equation of (*).
Then a^(p)_n can be foun in the form Q(n)\times s^n, where Q(n) is a polynomial (with unknown coefficients) of the same degree as P(n).
(2.) S is a root of multiplicity m of the characteristic equation.
Then a^(p)_n can be found in the form n^m\times Q(n)\times s^n, where Q(n) is a polynomial (with unknown coefficients) of the same degree as P(n).
Ex. Find a general solution of a_n = 5a_{n-1} - 6a_{n-1} - 6a_{n-2} + 7^n
(1.) a_n = 5a_{n-1} - 6a_{n-2}
r^2 - 5r + 6 = 0
r_1 = 2, r_2 = 3.
a^(h)_n = b_1 \times 2^n + b_2 \ times 3^n
(2.) a^(p)_n = C\times 7^n (plug this into (*))
C\times 7^n = 5(C7^{n-1})-6(C^{n-2})+7^n (Cancel 7^{n-2}
49 C = 35C - 6C + 49
C= 49/20
a^(p)_n - (49/20) \times 7^n
a_n = a^(h)_n + a^(p)_n = b_1(2^n) + b_2(3^n) + (49/20)(7^n)
QED.
10/13/2015
Chapter 10: Graphs
Directed graphs.
Cyclic graphs C_n, n >= 3
Wheels W_n, n>= 3
Adjacent vertices. Incident edge to vertices.
The Adjacency matrix: A_g of a graph g is an nxn matrix (where n is the number of vertices) such that: a_ij = #edges connecting v_i and v_j.
If no two vertices of G are connected by more than one edge and if G has no loops, then G is called a simple graph.
Important: The degree of a vertex v is the number of edges incident to v. Note: a loop at v contributes 2 to the degree of v. deg. v.
Complete Graphs K_n: a simple graph of n vertices, n >= 2, where any two vertices are connected by an edge.
K_n has C(n,2) edges = n(n-1)/2. Degree of every vertex of K_n = n-1.
10/15/2015
HW #7
p.665, Ex. 5, 18, 21, 22, 26, 38, 41
P.675, Ex. 5, 6, 7, 11, 12, 15, 35-42
10.2 The "Handshaking lemma" (pg. 653: The Handshaking Theorem)
Sum of deg(v) = 2m
Proof: Let e_ij be an edge connecting vertex v_i to vertex v_j, v_i != v_j.
On the left-hand side of the formula, we count e_ij exactly twice:
When we compute deg(v_i) and when we compute deg(v_j), if e_0 is a loop at vertex v_o, we count it twice when we compute deg(v_0), just by the definition of degree.
Corollary: Any (undirected) graph has an even number of vertices of odd degree.
Proof: Sum deg(vi) = sum_even deg(vi) + sum_odd deg(vi) = 2m
If we had an odd number of vertices of odd degree, the sum_odd deg(vi) would be odd, so the whole sum deg(vi) would be odd, too, which is a contradiction because it should equal 2m.
Corollary: The number of people who exchanged an odd number of handshakes in their lifetime, is even.
Diagraphs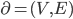 , every edge is an ordered pair of vertices
, every edge is an ordered pair of vertices 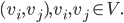 . v_i is called the initial vertex of such an edge, and v_j the terminal vertex.
. v_i is called the initial vertex of such an edge, and v_j the terminal vertex.
In a diagraph
For a vertex v_o of a diagraph =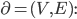
- the out-degree of v_o (deg_out (v_o)) is the number of edges incident to v_o is the initial vertex.
- the in-degree of v_o (deg_in (v_o)) is the....terminal vertex.
Adjacency matrix of a digraph deals with edges from vi to vj, for matrix A = a_ij.
Bipartite graphs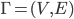 is called by partite if its vertex set V can be split in a disjoint union of vertex sets:
is called by partite if its vertex set V can be split in a disjoint union of vertex sets: 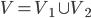 , such that no two vertices in V_1 are adjacent and no two vertices in V_2 are adjacent.
, such that no two vertices in V_1 are adjacent and no two vertices in V_2 are adjacent.
----------------
A graph
Conjecture: For even n, Cn is bipartite, for odd n; Cn is not.
i) let n be even, n = 2k, k >= 2. Enumerate vertices of Cn, starting with any vertex going clockwise, by numbers from 1 to 2k.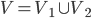
Now let the vertex set V_1 contain all the odd-numbered vertices:
V_1 = {v1,v3, ..., v_2k-1} and let V_2 contain all the even-numbered vertices:
V_2 = {v2,v4, ..., v_2k} V_1 and V_2 are obviously disjoint, and
Furthermore, vertices in V_1 are only adjacent to vertices in V_2, and vertices in V_2 are only adjacent to vertices of V_1.
ii) let n be odd, n=2k+1. By way of contradiction, assume that C_2k+1 is bipartite.
Starting at any vertex v_1, assign this vertex to a set V_1. Then adjacent vertices, v_2 and v_2k+1, should be assigned to the other set, V_2. Continuing with this assignment, we see that vertices v_i with odd i should be assigned to the set V_1. But then v_1 and v_2k+1 will both be assigned to V_1. Since these two vertices are adjacent, we get a contradiction.
Graph isomorphism
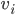 and
and 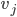 are adjacent in
are adjacent in 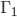 , then
, then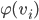 and
and 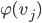 are adjacent in
are adjacent in 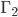 .
.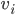 and
and 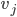 are not adjacent in
are not adjacent in 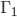 , then
, then 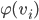 and
and 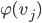 are not adjacent in
are not adjacent in 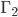 .
.
==================
let
1). if vertices
2). if
Note: If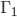 and
and 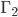 are isomorphic, then they have
are isomorphic, then they have
1.) the same number of vertices.
2.) the same number of edges.
10/20/2015
HW #8
p.677, Ex. 54, 56
p.689, Ex. 3-6, 11, 21, 22, 23
Someone raised a question for solving #11 in page 511. Prof. skipped it saying it's a lot of thinking.
Exercises in class: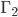 , every vertex of degree 1 is adjacent to a vertex of degree 3, whereas in
, every vertex of degree 1 is adjacent to a vertex of degree 3, whereas in 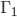 , there is a vertex of degree 1 that is not adjacent to any vertex of degree 3.
, there is a vertex of degree 1 that is not adjacent to any vertex of degree 3. 
Pg. 677: #41,
Solution: In
#42.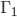 , vertices of degree 4 are adjacent, whereas in
, vertices of degree 4 are adjacent, whereas in 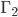 , they are not.
, they are not. 
Solution: In
#43.
Do mapping of vertices. It is isomorphic.
10.4 Connectivity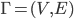 is a sequence of edges
is a sequence of edges 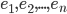 such that, if
such that, if 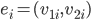 , then
, then 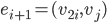 .
. is called connected if any two vertices of
is called connected if any two vertices of  can be connected by a path.
can be connected by a path. is connected, then for any two vertices
is connected, then for any two vertices 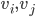 of
of  , there is a simple path connecting
, there is a simple path connecting 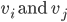 .
.
A path in a graph
A path is called simple if no edge occurs more than once in this path.
A graph
If a graph is not connected, then it is called disconnected.
Theorem: If a graph
Lemma: If a connected graph \Gamma has a circuit, we can remove any edge from this circuit, and \Gamma will still be connected.
Proven on the board.
Proof of theorem: By the lemma, we can get rid of all the circuits in , by removing one edge at a time, and
, by removing one edge at a time, and  will still be connected.
will still be connected. that connects some
that connects some 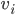 to some
to some 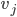 . If this path does not have backtracking, then it is a simple path and we are done.
. If this path does not have backtracking, then it is a simple path and we are done.
In a graph without circuits, any path (without backtracking) is a simple path. Now suppose there is a path in
If there is a backtracking along this path, just eliminate it, and this will produce a simple graph.
A connected component of graph is a maximal connected subgraph of
is a maximal connected subgraph of  .
. to this subraph, it will become disconnected.
to this subraph, it will become disconnected.
"Maximal" means that if you add any other edge of
A single vertex which is a connected component is called an isolated vertex.
Let be a graph. A vertex
be a graph. A vertex 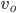 of
of  is called a cut vertex
is called a cut vertex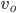 together with all incident edges from
together with all incident edges from  , the number of connected components in
, the number of connected components in  increases.
increases.
if, after removing
Same case with cut edge. Except we remove nothing else but the cut edge.
It is also called a bridge.
10/22/2015 is a separating set if after you remove all vertices from this set together with all incident edges, the number of connected components of
is a separating set if after you remove all vertices from this set together with all incident edges, the number of connected components of  increases.
increases.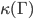 , of a graph
, of a graph  is the minimum cardinality of a separating set.
is the minimum cardinality of a separating set.
A set of vertices of a graph
The vertex connectivity,
(pg. 684)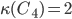 , more generally,
, more generally, 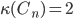
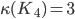 , more generally,
, more generally, 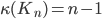
Ex.
Ex.
Ex.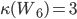 .
.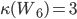
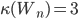
Proof: We cannot make W6 disconnected without removing the central vertex. Removing it produces a cycle graph. Removing a single vertex from a cycle graph cannot make it disconnected, but removing two vertices can.
Therefore,
more generally,
Let be a connected graph. An edge cut of
be a connected graph. An edge cut of  is a set of edges of
is a set of edges of  such that, if you remove this set from
such that, if you remove this set from 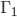 it becomes disconnected.
it becomes disconnected.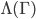 , of a graph
, of a graph  is the minimum cardinality of an edge cut.
is the minimum cardinality of an edge cut.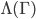 same as vertex connectivity.
same as vertex connectivity.
Edge connectivity,
examples for
Remark: Let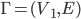 be connected then
be connected then 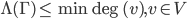 .
.
pg. 687
 .
.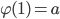 ,
, 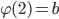 ,
, 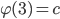 .
. , have to be pairwise adjacent because 1, 2, 3 in
, have to be pairwise adjacent because 1, 2, 3 in 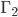 are pairwise adjacent. That means, there is a circuit of length 3 in
are pairwise adjacent. That means, there is a circuit of length 3 in 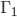 , a contradiction.
, a contradiction.
Example 14, figure 6.
Claim:
Proof: By way of contradiction, supopse there is an isomorphism
Let
Then the vertices a, b, c of the graph
Same Ex. figure 7.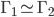
Try all mapping.
Counting paths between vertices
===============================
Theorem 2, pg. 688
10/27/2015
Solution for HW problems pg. 665 #18:
Suppose our graph has n vertices. Then the maximum degree of a vertex is n-1. Consider two cases:
1. graph does not have isolated vertices. Then possible degrees of vertices are: 1, 2, ... , n-1. (altogether n-1 possibilities). Then, by the pigeonhole principle, at least 2 vertices must have the same degree.
2. graph does have an isolated vertex. Then possible degrees are: 0,1,2,...,n-2 (altogether n-1 possibilities). By the pigeonhole principle there must be at least 2 vertices of the same degree.
To Show Isomorphism:
1) # vertices
2) # edges
3) collection of degrees
4) adjacencies of vertices of the corresponding degrees
5) collection of circuit lengths
these would suffice for now.
11/03/2015
HW #9
p.703, Ex. 2, 3, 5, 7, 10, 15, 28, 30, 31, 32, 36, 42
Tu, 11/10 - no class
Exam 2
Average: 33/50
>= 40, A
>= 36, B
>= 31, C
Exam 2 #5 k vertices has at least n-1 edges
k vertices has at least n-1 edges be a connected graph on k+1 vertices.
be a connected graph on k+1 vertices.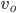 be a vertex of degree m in
be a vertex of degree m in  .
.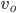 together with all incident edges.
together with all incident edges.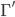 has at least
has at least 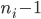 edges, where
edges, where 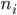 is the number of vertices in that component. Summing up over all connected components of the
is the number of vertices in that component. Summing up over all connected components of the 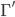 , we get at least
, we get at least 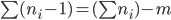 edges in
edges in 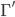 .
.  .
. itself has at least (k-m)+m = k edges. This completes the proof.
itself has at least (k-m)+m = k edges. This completes the proof.
Prove that every connected graph on n vertices has at least n-1 edges.
Induction by n.
a) base n=2,
b) suppose any connected graph on
Let
Let
Remove
The remaining graph has at most m connected components.
By the inductive assumption, each connected component of the
That means
Another proof of the induction step: has degree
has degree 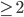 , then
, then  has a circuit.
has a circuit. as follows. Start at any vertex
as follows. Start at any vertex 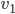 and move along any edge incident to
and move along any edge incident to 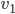 . You will arrive at a vertex
. You will arrive at a vertex 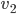 .
.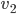 has degree at least 2, you can leave
has degree at least 2, you can leave 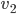 using a different edge than the one you used to arrive at
using a different edge than the one you used to arrive at 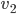 . Continuing this process, you will eventually arrive at a vertex that you have visited before, this creating a circuit.
. Continuing this process, you will eventually arrive at a vertex that you have visited before, this creating a circuit. has a circuit, we can remove an edge from this circuit, and
has a circuit, we can remove an edge from this circuit, and  will still be connected.
will still be connected. .
.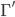 will still be connected, so we can just use the inductive assumption for
will still be connected, so we can just use the inductive assumption for 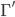 .
.
Lemma: if every vertex in a connected graph
Proof: Build a circuit in
Since
If
Continue this until there is a vertex of degree 1 in
Then the induction step is easy: remove a vertex of degree 1 together with the incident edge, and the remaining graph
Another proof is by simultaneous induction.
CUNYFIRST was USD 700Mil?!
10.5 Eulerian graphs be a connected graph. An Eulerian circuit is a simple circuit that contains all edges of
be a connected graph. An Eulerian circuit is a simple circuit that contains all edges of  . An Eulerian path is a simple path that contains all edges of
. An Eulerian path is a simple path that contains all edges of  .
. is called Eulerian if it has an Eulerian circuit, and is called semi-Eulerian if it has an Eulerian path but no Eulerian circuits.
is called Eulerian if it has an Eulerian circuit, and is called semi-Eulerian if it has an Eulerian path but no Eulerian circuits.
Let
A graph
Theorem: A connected graph is Eulerian if an only if every vertex of
is Eulerian if an only if every vertex of  has even degree.
has even degree. is semi-Eulerian if and only if it has exactly 2 vertices of odd degree.
is semi-Eulerian if and only if it has exactly 2 vertices of odd degree.
Theorem: A connected graph
11/05/2015
HW #10
p. 732, Ex. 5-12,15,28
Fleury's algorithm
For finding an Eulerian circuit in an Eulerian graph.
1) Choose any edge
2) Once an edge is chosen:
-- a) remove it
-- b) choose any edge adjacent to it, but choose a cut edge only if there is no other choice.
3) Repeat until all edges are chosen.
Hamiltonian Graphs be a connected graph. A Hamiltonian circuit in
be a connected graph. A Hamiltonian circuit in  is a circuit that passes through every vertex of
is a circuit that passes through every vertex of  exactly once.
exactly once. is a path that passes through every vertex exactly once.
is a path that passes through every vertex exactly once. is Hamiltonian if it has a Hamiltonian circuit, and it is semi-Hamiltonian if it has a Hamiltonian path but no Hamiltonian circuit.
is Hamiltonian if it has a Hamiltonian circuit, and it is semi-Hamiltonian if it has a Hamiltonian path but no Hamiltonian circuit.
Let
A Hamiltonian path in
A Connected graph
Ex.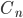 , n
, n 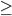 3, is Hamiltonian.
3, is Hamiltonian.
Ex.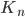 , n
, n 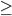 3, is Hamiltonian.
3, is Hamiltonian. has a Hamiltonian subgraph on the same set of vertices, then
has a Hamiltonian subgraph on the same set of vertices, then  itself is Hamiltonian.
itself is Hamiltonian.
Remark: If
Ex.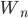 , n
, n 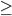 3, is Hamiltonian because
3, is Hamiltonian because 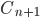 is a subgraph of
is a subgraph of 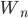 on the same set of vertices.
on the same set of vertices.
NP-Complete, Complexity in Computer Science: uses Hamiltonian graphs.
Theorem: If a connected simple graph has n vertices and the degree of every vertex is
has n vertices and the degree of every vertex is 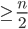 , then
, then  is Hamiltonian.
is Hamiltonian. to be Hamiltonian.
to be Hamiltonian.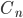 , the degree of every vertex is 2, and yet it is Hamiltonian for any
, the degree of every vertex is 2, and yet it is Hamiltonian for any 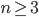 .
.
Remark: This condition is sufficient but not necessary for
Ex:
Theorem: If a connected simple graph has n vertices and for any pair of vertices
has n vertices and for any pair of vertices 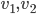 ,
, 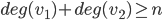 , then
, then  is Hamiltonian.
is Hamiltonian.
Remark: A graph that has a cut edge cannot be Hamiltonian. has a cut vertex, then it cannot be Hamiltonian.
has a cut vertex, then it cannot be Hamiltonian.
Remark: If
Many have tried to find a way (e.g. algorithm) to find Hamiltonian graph but failed, hence the 1Mil award.
Exercise. 34, pg. 705 is challenging. Brute force suggested.
Exercise. 35, By way contradiction, suppose there is a Hamilton circuit. Then, without loss of generality, we can start this circuit at d and go to b. By the symmetry, we can now go to either a or e.
Let's go to a. Then we have to go to c. If we now go to d, we will complete a circuit without visiting e. If we go to e, we then will have to go to 2, thus visiting it twice before completing a circuit. This contradiction proves that the graph is not Hamiltonian.
Next 10.8, Chapter 11. Trees
11/17/2015
Next Tues (11/24) Quiz (no Eulerian graphs, but Hamiltonian graphs, maybe coloring.) 30 mins.
Test 3: 12/8 (TUES): 10.3, 10.4,
10.5,10.8, 11.1, 11.4, 11.5(test hint: Something about proving a rooted tree by induction)
10.8 Graph Coloring , so that no two adjacent vertices of
, so that no two adjacent vertices of  have the same color.
have the same color. is called the chromatic number of
is called the chromatic number of  ,
, 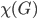 .
.
Graph coloring is assigning a color to every vertex of a given graph
---------
The minimum number of colors required for coloring a graph
Examples:
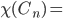 2, if n is even; 3, if n is odd.
2, if n is even; 3, if n is odd.
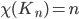
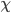 (Bipartite graphs) = 2. Converse is true as well: A graph
(Bipartite graphs) = 2. Converse is true as well: A graph  is bipartite iff
is bipartite iff 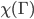 = 2.
= 2.
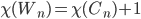 = 3 if n is even; 4, if n is odd.
= 3 if n is even; 4, if n is odd.
===========
An Edge coloring of a graph is assigning a color to every edge of
is assigning a color to every edge of  so that no edges incident to the same vertex are assigned the same color.
so that no edges incident to the same vertex are assigned the same color. is called the edge chromatic number of
is called the edge chromatic number of 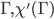 .
.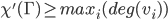
===========
The minimum number of colors required to edge color
Remark:
Examples:
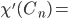 2 if n is even; 3 if n is odd.
2 if n is even; 3 if n is odd.
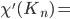 ? Homework.
? Homework.
============
11.1 Trees is called a tree if it is connected and has no circuits.
is called a tree if it is connected and has no circuits.
A graph
Theorem: A graph on n vertices is a tree if and only if it is connected and has (n-1) edges.
on n vertices is a tree if and only if it is connected and has (n-1) edges. be a tree on n vertices. Then
be a tree on n vertices. Then  is connected.
is connected.
Proof: (1) "only if". Let
By problem 5 on test 2, has at least (n-1) edges.
has at least (n-1) edges.
Lemma: If a graph on n vertices has
on n vertices has 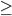 edges, then
edges, then  has a circuit.
has a circuit.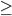 k edges has a circuit, for any k
k edges has a circuit, for any k  n. Let
n. Let  have n+1 vertices and
have n+1 vertices and 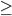 n+1 edges. If
n+1 edges. If  has a circuit, then there is nothing to prove.
has a circuit, then there is nothing to prove. does not have any circuits, then
does not have any circuits, then  should have a vertex of degree 1.
should have a vertex of degree 1. . The remaining graph,
. The remaining graph,  , has n vertices and
, has n vertices and 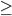 n edges. By the inductive assumption,
n edges. By the inductive assumption,  has a circuit, and therefore
has a circuit, and therefore  has a circuit, too. This completes the proof by induction.
has a circuit, too. This completes the proof by induction.
Proof: Induction on n.
(1) n = 2 - obvious.
(2) Suppose any graph with k vertices and
If
Remove this vertex, together with the incident edge, from the graph
(2) "if" Let be a connected graph with n vertices and (n-1) edges. We have to prove that
be a connected graph with n vertices and (n-1) edges. We have to prove that  is a tree. By way of contradiction, suppose
is a tree. By way of contradiction, suppose  has a circuit. Then we can remove any edge from this circuit, and the remaining
has a circuit. Then we can remove any edge from this circuit, and the remaining 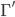 will still be connected. But
will still be connected. But 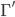 has n vertices and (n-2) edges and therefore cannot be connected (by Problem 5 on test 2). This contradiction completes the proof.
has n vertices and (n-2) edges and therefore cannot be connected (by Problem 5 on test 2). This contradiction completes the proof.
Rooted Trees
Any tree is a rooted tree!
Root = level 0.
Vertices that have no "children" are called leaves.
A (rooted) tree is k-regular if every vertex, other than a leaf, has exactly k children.
A 2-regular tree is also called a binary tree.
The number of levels in a rooted tree is called its height.
11/19/2015
HW #11
p.755, ex. 3, 9, 11, 12(a), 14, 16, 19
p.795, ex. 2-6
11.4 Spanning tree be a simple graph. A spanning tree of
be a simple graph. A spanning tree of  is a subgraph of
is a subgraph of  that includes all vertices of
that includes all vertices of  and is a tree.
and is a tree.
Let
!Spanning tree is not unique.
Depth-first algorithm ("backtracking")
for constructing a spanning tree
Algorithm .
.
1) Start with any vertex
2) From the current vertex, go along any incident edge as long as this does not create a circuit.
3) If you cannot go anywhere without creating a circuit, then backtrack and repeat.
4) stop when you have visited all vertices of
Breadth-first search algorithm
Algorithm
1) Start with any vertex, this is the root.
2) While at a current vertex, select all edges incident to this vertex, that were not previously used. This builds the next level of the rooted tree.
3) Stop when all vertices have been visited.
Example: When should an edge of a simple graph be in every spanning tree of this graph?
ans: cut edge.
Example: Let be a connected simple graph. Suppose an edge e is contained in every spanning tree of
be a connected simple graph. Suppose an edge e is contained in every spanning tree of  . Is it true that e is a cut edge?
. Is it true that e is a cut edge?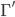 is still connected and includes all vertices of
is still connected and includes all vertices of  . Therefore,
. Therefore, 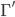 is a spanning tree that includes all vertices of
is a spanning tree that includes all vertices of  and does not include the edge e.
and does not include the edge e. that does not include e, a contradiction.
that does not include e, a contradiction.
Yes.
Proof: By way of contradiction, suppose e is not a cut edge. Remove e. The remaining graph
Thus, we get a spanning tree for
12/01/2015
HW#12
p. 795, Ex. 14, 15, 16, 17(c), 39, 44
p. 802, Ex. 4, 7
Past HW, p. 755, #14 be a tree. Then
be a tree. Then  is connected.
is connected. have n vertices. Then it has (n-1) edges.
have n vertices. Then it has (n-1) edges.
Show that a simple graph is a tree IFF it is connected but deleting any of its edges produces a graph that is disconnected.
--
(1) The "only if" part: Let
Let
Removing any edge produces a graph with n vertices and (n-2) edges. A graph like that cannot be connected by problem 5 on test 2.
(2) The "if" part: Let Γ be a simple connected graph, such that removing any edge from Γ produces a disconnected graph.
What we have to prove is that Γ has no circuits (because the fact that Γ is connected is given).
By way of contradiction, assume Γ has a circuit C. Removing any edge from C will keep Γ connected, a contradiction.
11.5 Minimum spanning trees
[Fig. 3] problem: Find a spanning tree with minimal total weight of its edges (a minimum spanning tree)
--- Prim's algorithm
(1) Choose any edge of minimum weight
(2) Choose any edge of minimum weight among edges incident to vertices that are already included in our spanning tree, but do not create a circuit!
--- Kruskal's Algorithm
(1) Choose any edge of minimum weight
(2) Choose any edge of minimum weight , but do not create a circuit!
p.805 #3
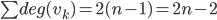
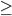 2.
2.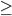 2 is
2 is 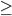 2(n-1).
2(n-1).
Show that if a tree has at least one edge, then it has at least two pendant vertices (i.e. vertices of degree 1).
---
Let a tree Γ have n vertices. Then it has (n-1) edges. By the handshaking lemma:
By way of contradiction, assume there is one or no vertices of degree 1.
Then there are at least n-1 vertices of degree
The sum of the degrees of (n-1) vertices of degree
The remaining vertex cannot have degree 0. Therefore, the total sum of the degrees is at least 2(n-1)+1 = 2n-1 > 2n-2,
a contradiction.
#4 Show that a tree with n vertices that has (n-1) pendant vertices must be isomorphic to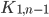 .
.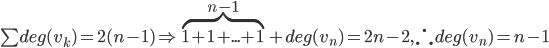
----
Use diagram,
12/03/2015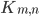 are trees?
are trees?
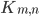 is connected for any m, n >= 1.
is connected for any m, n >= 1.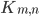 is a tree IFF m=1 or n=1.
is a tree IFF m=1 or n=1.
p.756, # 16: Which complete bipartite graphs
Circuits: Let m, n >= 2. show diagram and circuit path.
So, m = 1 or n = 1 is a tree.
Answer:
p.796, #39: Which connected simple graphs have exactly one spanning tree?
(1) Any tree has exactly one spanning tree (itself)
(2) if the graph is connected but not a tree, then it has a circuit C with more than 2 edges. Since any edge can be removed from C while keeping the graph connected, we'll have at least 3 different spanning trees for the graph if we start by removing different edges from C.
Claim: Let Γ be a connected simple graph with a circuit C. Let e be an arbitrary edge. Then Γ has a spanning tree that contains e.
We construct a spanning tree by removing edges from circuits of Γ. Every time we want to remove an edge from a circuit containing e, we remove an edge different than e.
Then e will be contained in the final spanning tree.
p805. #6: Suppose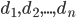 are positive integers that sum up to 2n-2. Show that there is a tree on n vertices such that degrees of vertices are
are positive integers that sum up to 2n-2. Show that there is a tree on n vertices such that degrees of vertices are 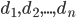 .
.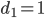 ,
,
Let
Induction by the number of vertices.
#7: Prove that every tree is a planar graph (A graph that can be drawn on a plane so that its edges don't intersect at points other than vertices). at level n, draw its children at level n+1 in the corresponding space between vertical lines. Then edges connecting parents at level n to children at level n+1 will not intersect. This completes the proof by induction.
at level n, draw its children at level n+1 in the corresponding space between vertical lines. Then edges connecting parents at level n to children at level n+1 will not intersect. This completes the proof by induction.
Proof: Any tree is a rooted tree.
Induction by the number of levels in a rooted tree.
(1) one level: a root connected to k leaves. This graph is planar.
(2) Suppose any rooted tree with n >= 1 levels is planar.
Let T be a rooted tree with n+1 levels.
By the inductive assumption, we can draw the first n levels of T so that edges don't intersect.
Separate vertices at level n by vertical lines: show diagram.
For each vertex