Professor: Benjamin Steinberg
HW must be from 8th edition of textbook.
Set-builder notation.
Empty set is contained in all sets.
A = B, if 
{a,b,c} = {a,a,b,b,c,c,c}
Theorems and Definitions of the text: (variables are generally assumed to be integers unless stated otherwise)
Chapter 1 Fundamentals
Section 1.1 Sets
Section 1.2 Mappings
Section 1.3 Properties of Composite Mappings (Optional)
Section 1.4 Binary Operations
Section 1.5 Permutations and Inverses
Section 1.6 Matrices
Section 1.7 Relations
Chapter 2 The Integers
Section 2.1 Postulates for the Integers (Optional)
Section 2.2 Mathematical Induction
Section 2.3 Divisibility
Section 2.4 Prime Factors and GCD
Definition 2.11 Greatest Common Divisor: gcd(a,b) = d
1. d > 0
2. d|a & d|b
3. c|a & c|b => c|d
Theorem 2.12 Greatest Common Divisor
A method to find gcd: Euclidean Algorithm
Definition 2.13 Relatively Prime Integers: gcd(a,b) = 1
Theorem 2.14 If gcd(a,b) = 1 & a|bc => a|c
Definition 2.15 Prime Integer (p)
1. p > 1
2. the only divisors of p: ± 1 and ±p
Theorem 2.16 Euclid's Lemma
prime p |ab,
=> either p|a or p|b
Corollary 2.17 prime p|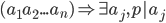
Theorem 2.18 Unique Factorization Theorem = Fundamental Theorem of Arithmetic
n > 0,
=> n=1 or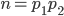 
..., where 
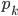are unique primes
Terms: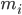 
= multiplicity of 
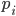=> standard form for 
...
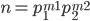Definition 2.19 Least Common Multiple: lcm(a,b) = m where a, b != 0
1. m > 0
2. a|m & b|m
3. a|c & b|c => m|c
Theorem 2.20 Euclid's Theorem: The number of primes is infinite
Section 2.5 Congruence of Integers
Definition 2.21 Congruence modulo n
n > 1, x ≡ y (mod n)
Theorem 2.22 Congruence modulo n is an equivalence relation on Z.
Congruence classes = residue classes
Theorem 2.23 Addition and Multiplication Properties
a ≡ b (mod n),
=> a+x ≡ b+x (mod n) & ax ≡ bx (mod n)
Theorem 2.24 Substitution Properties
a ≡ b (mod n) & c ≡ d (mod n),
=> a+c ≡ b+d (mod n) & ac ≡ bd (mod n)
Theorem 2.25 Cancellation Law
gcd(a,n) = 1 & ax ≡ ay (mod n),
=> x ≡ y (mod n)
Theorem 2.26 Linear Congruences
gcd(a,n) = 1,
∃x =>ax = b (mod n)
=> 
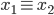(mod n)
Theorem 2.27 System of Congruences
gcd(m,n) = 1,
∃x => x ≡ a (mod m), x ≡ b (mod n),
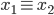=> (mod mn)
Theorem 2.28 Chinese Remainder Theorem
expands theorem 2.27
Section 2.6 Congruence Classes: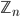 
= {[0],[1],...,[n-1]}
Theorem 2.29 Addition in 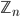: [a] + [b] = [a+b]
1. Associative & commutative in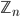
2. [0] = additive identity
3. [-a] is additive inverse of [a], where [-a],[a]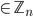 
Theorem 2.30 Multiplication in 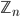: [a][b] = [ab]
1. Associative & Commutative in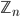
2. [1] = multiplicative identity
3. Theorem 2.31 [a] 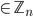has multiplicative inverse in 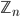IFF gcd(a,n) = 1
Corollary 2.32 [a] in 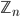has multiplicative inverse IFF n is a prime
Section 2.7 Introduction to Coding Theory (Optional) - skipped
Section 2.8 Introduction to Cryptography (Optional)
Theorem 2.33 RSA Public Key Cryptosystem
Chapter 3 Groups
Section 3.1 Definition of Group
Definition 3.1 Group, G
1. G is Closed under *
2. * is associative
3. G has identity element e
4. all elements of G has inverses in G
Definition 3.2 Abelian Group (=Commutative group)
Definition 3.3 Finite, Infinite groups, Order of Group (|G|)
Section 3.2 Properties of Group Elements
Theorem 3.4 Properties of Group Elements
1. e in G is unique
2. All inverses of elements in G are in G and unique
3. 
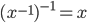
4. 
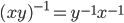Reverse order law
5. ax = ay or xa = ya imples x = y: Cancellation law
Theorem 3.5 Equivalent Conditions for a Group
G is nonempty set, closed under associative multiplication.
G is a group IFF ax = b and ya = b s.t. x and y in G, for all a and b in G.
Definition 3.6 Product Notation
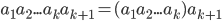for 
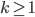
Theorem 3.7 Generalized Associative Law
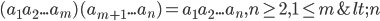
Definition 3.8 Integral Exponents
Compare Multiplicative and Additive Notations
Theorem 3.9 Laws of Exponents
1. 
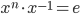
2. 
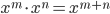
3. 
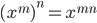
4. 
Can be translated to Laws of Multiples for additive groups.
Section 3.3 Subgroups
Definition 3.10
Theorem 3.11 Subgroup, H 
G is a subgroup IFF:
1.) identity e is in H (H is nonempty)
2.) H is closed under *
3.) 
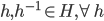, closed under inverse
Notation: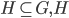 
is a subgroup of G
Theorem 3.12 Equivalent Set of Conditions for a Subgroup (Summarized Theorem 3.11)
H is subgroup of IFF:
1. H is nonempty (I think this can be ignored)
2. a, b in H implies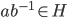 
Definition 3.13 The center of a Group
Z(G) = {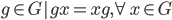
}
Meaning all g which commute with every element of G
Theorem 3.14 The center of a group G is an abelian subgroup of G
Definition 3.15 The Centralizer of a Group Element
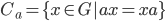
Theorem 3.16 The centralizer of a in G is a subgroup of G
Definition 3.17 Cyclic Subgroup
For any a in group G, <a> = subgroup generated by a =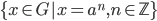 
= H = cyclic subgroup of G. The element a is called a generator of H.
Section 3.4 Cyclic Groups
Definition 3.18 Generator (repeated from last section)
Theorem 3.19 Infinite Cyclic Group
If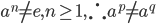 
whenever 
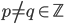and <a> is an infinite cyclic group
Corollary 3.20 If G is a finite group, then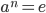 
for some positive integer n.
Theorem 3.21 Finite Cyclic Group
If m is the least positive integer s.t. a^m = e, then
1. <a> has order m
2. 
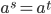IFF 
(mod m)
Definition 3.22 Order of an Element: o(a) = |a| = |<a>|
Order of Subgroup of G generated by a in G
Corollary 3.23 Finite Order of an Element
If |a| is finite, then m = |a| is the least positive integer s.t.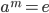 
Theorem 3.24 Subgroup of a Cyclic Group
If H is a subgroup of cyclic group G with generator a, then
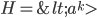, where k is the least positive integer s.t.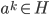 
Corollary 3.25 Any subgroup of a cyclic group is cyclic
Theorem 3.26 Generators of Subgroups
Subgroup (generated by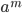 
) of cyclic group of order n generated by a = subgroup generated by 
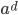, where d = gcd(m,n)
Corollary 3.27 Distinct Subgroups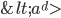 
of a Finite Cyclic Group, G
where d is a positive divisor of n.
Theorem 3.28 Generators of a Finite Cyclic Group <a>:
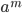is a generator of <a> of order n IFF gcd(m,n) = 1
Section 3.5 Isomorphisms
Definition 3.29 Isomorphism, Automorphism
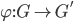is an isomorphism from G to G' if:
1. 
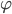is a bijection from G to G'
2. 
Notation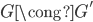 
Automorphism: An isomorphism from G to G
Theorem 3.30 Images of Identities and Inverses
1. 
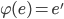and
2. 
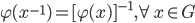
Section 3.6 Homomorphisms
Definition 3.31 Groups G,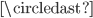
& G'',
, Homomorphism: 
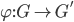s.t. 
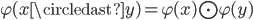or
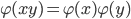
1. Endomorphism: G = G'
2. Epimorphism: 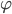is onto, G' is homomorphic image of G.
3. Monomorphism: 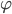is one-to-one
Theorem 3.32 Images of Identities and Inverses (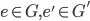
)
1.
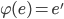
2.
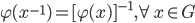
Definition 3.33 Kernel: ker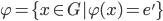 
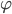is a homomorphism from group G to G'
Chapter 4 More on Groups
Section 4.1 Finite Permutation Groups
Definition 4.1 Cycle
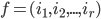
This statement is not unique.
Disjoint subsets which define cycles, are called orbits
Theorem 4.2 Partition of A
Definition 4.3 Orbit
Let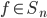 
, the orbit of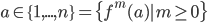 
The orbits form a partition of {1,...,n}
Note: All permutations can be written as a product of transpositions:
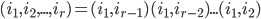
Lemma 4.4 t(P) = (-1)P
t is any transposition (r,s) on {1,2,...,n} and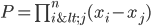 
Theorem 4.5 Products of Transpositions (Either all even or all odd transpositions)
Definition 4.6 Even Permutation vs. Odd Permutation (based on number of transpositions)
Even Permutation if r in r-cycle is odd
Odd Permutation if r in r-cycle is even
Definition 4.7 Alternating Group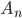 
is the subgroup of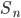 
that consists all even permutations in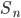
Definition 4.8 Conjugate Elements
1. The Conjugate of a by b is the element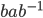 
2. c is a conjugate of a IFF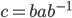 
for some b in G
Section 4.2 Cayley's Theorem
Definition 4.9 Cayley's Theorem
Every group is isomorphic to a group of permutations.
Section 4.4 Cosets of a Subgroup
Definition 4.10 Product of Subsets
Let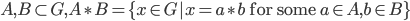 
Theorem 4.11 Properties of the Product of Subsets
1. Associative
2. not commutative
3. B = C 
AB = AC & BA = CA
4. AB = A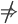C 
B = C
5. gA = gB A = B
Definition 4.12 Cosets, H < G,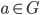 
Left coset of H in G: aH = {
| x = ah for some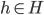 
}
Right coset of H in G: Ha
Left & right cosets are never disjoint, but they may be different sets.
Lemma 4.13 Left Coset Partition
The distinct left cosets of H form a partition of G.
Definition 4.14 Index: [G:H]
The total number of distinct left cosets of H in G.
Theorem 4.15 Lagrange's Theorem
If G is a finite group,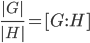 
Corollary 4.16 |a| divides |G|
Section 4.5 Normal Subgroups
Definition 4.17 Normal (Invariant) Subgroup
H is a normal subgroup of G if xH = Hx for all x in G (left coset = right coset)
Note that it does not mean xh = hx
Theorem 4.18 A special coset H: hH = Hh = H
Corollary 4.19 The square of a subgroup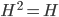 
Theorem 4.20 Normal Subgroups and Conjugates
H is a normal subgroup of G IFF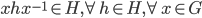 
Definition 4.21 Set Generated by A
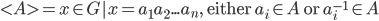
Theorem 4.22 Subgroup Generated by A: <A> is a subgroup of G generated by A
Section 4.6 Quotient Groups
Theorem 4.23 Group of Cosets
If H is normal subgroup of G, then cosets of H form a group with respect to the product of subsets
Definition 4.24 Quotient (Factor) Group of G by H
If H is normal subgroup of G, the group G/H consists of the cosets of H in G is the quotient group of G by H
Theorem 4.25 Quotient Group => Homomorphic Image
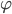(a) = aH is an epimorphism from G to G/H
Theorem 4.26 Kernel of a Homomorphism
If f is a homomorphism from G to G', ker f is a normal subgroup of G
Theorem 4.27 Homomorphic Image => Quotient Group
Let G and G' be groups with G' a homomorphic image of G. Then G' is isomorphic to aquotient group of G
Theorem 4.28 Fundamental Theorem of Homomorphisms
If 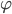is an epimorphism from the group G to the group G', then G' is isomorphic to G/ker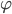
Skipped
Chapter 5 Rings, Integral Domains and Fields
Section 5.1 Definition of a Ring
Definition 5.1a A set R is a ring it has all 6 properties:
a) closed under + and .
b) associative under + and .
c) commutative under +
d) contains additive identity = zero = 0
e) contains additive inverses = -a = negative (opposite) of a, applies in subtraction
f) two distributive laws hold
Definition 5.1b Alternative Definition of a Ring:
a) R forms an abelian group under +
b) R is closed under associative multiplication
c) two distributive laws hold
Definition 5.2 Subring, analogous to subgroup
Theorem 5.3 Equivalent set of conditions for a subring
a) S is nonempty
b) x, y in S implies x+y and xy are in S
c) x in S implies -x in S
Theorem 5.4 Characterization of a subring
a) S is nonempty
b) x, y in S implies x-y and xy are in S
S = {0} and S = R are trivial subrings
subets, union, intersect.
favorite sets: integers, rationals, real, complex
Proofs: show what is Needed. Think of cases x in A, x in B, etc., in "or" (union) condition. In "And" (intersect) condition, may consider cases x in A, x not in A.
Propositions: associative, distributive, De Morgan Laws.
Partition of a set. A set is not a partition of itself.
pairwise disjoint = mutually disjoint.
Complement usually needs a context, in most case it's the Universal set. A' = U - A.
Power set.
02/03/2016
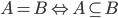and 
Review:
A partition of a set A is a collection of subsets of A which are:
1) not empty
2) pairwise disjoint
3) each element of A belongs to some element of the partition
Ordered pairs
If A, B are sets, the Cartesian (or direct)
product A X B =
|X| = size of X
|A x B| = |A| * |B|
Def: A function (or mapping) from A to B is a subset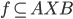
such that for all 
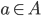there is a unique 
.
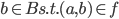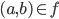, then write f(a) = b.
Notation: If
Passes the vertical line test.
interesting note:
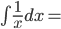
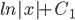, if x > 0
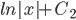, if x < 0
Domain, Codomain, Range (Range
Codomain) = image
Inverse Image of T,
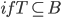
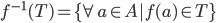
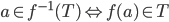
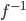is not a function
Inverse image may not necessary demand inverse function.
Warning:
Def: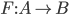
is onto or surjective if
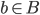is of the form f(a) with 
.
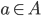range(f) = B. In words each
Def: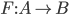
is one to one or injective if
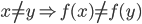
Passes the horizontal line test.
Hilbert's Hotel
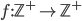
f(x) = x+1
is 1 to 1 but not onto
Note: If A, B are finite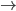
B is 1 to 1, then |A| 
|B|
B is onto, then |A| 
|B|
B is bijective, then |A| = |B|
1) f: A
2) f: A
3) f: A
02//08/2016
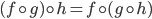
Associative
Proposition: If
then
pf: Both sides have domain A and codomain D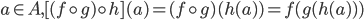
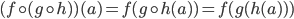
If
On the other hand
Proofs (theorems 1:16-17):
Prop A: The composition of onto functions is onto.
Prop B: The composition of one-to-one functions is one-to-one.
Binary operations: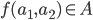
for all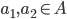 
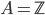
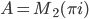= 2 x 2 real matrices
A binary operation on a set A is a mapping (function)
f: A X A -> A
so
Note: division is not a binary operator on integers, since division by zero is undefined.
X * Y = XY - YX
on
Properties of Binary operations:
- Associative
- Commutative (not always in life)
Light's associativity test mentioned. A way to test associativity on tables.
Commutative = symmetric across the diagonal on table.
2x2 matrices is assoc but not comm. Messy to prove assoc.
Definitions: Closure, identity, Inverse (right, left)
Note on Identity element: for operator "Or", F is identity (check if the order of row & column values are the same as the corresponding fields of the table).
Prop: If * is a binary operation an A, then if an identity exists, it must be unique.
Pf: Assume e, e' are identities.
Want e = e;
Have them battle, e*e' = e'
If e is the real identity,
e*e' = e, if e' is the real identity
So e = e*e' = e'
So there can be at most one.
Prop: If * is an assoc. binary op on A, then if a has a left inverse a' and a right inverse a''
then a' = a'' and so a has a unique inverse.
Compute: (a' * a) * a'' = e * a'' = a''
a' * (a * a'') = a' * e = a'
By assoc
(a' * a) * a'' = a' * (a * a'')
(a' * a) = a''
a * a'' = a'
a' = a'', is an inverse for a,
If a had two inverses take one to be a' and one to be a'' and get a' = a''.
02/10/2016
is a binary op on A. It is associative.
Identity function: i(x) = x, for all x, for the composition
f\circ i(x) = f(i(x)) = f(x)
So f\circ i = f
similarly i of (x) = i(f(x)) = f(x)
so i of f = f
so i is an identity.
Ex: X = all polynomials
D(p(x)) = p'(x)
I(p(x)) = \int_0^x p(t)dt
Are D, I inverses?
DI(p(X)) = p(x)
ID(x+2)= I(i)
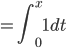
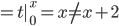
So D is a left inverse of I but not right inverse.
Permutations & Inverses
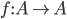is called a permutation
Def: A bijection
A permutation is a bijection from a set to itself.
S(A) = {all permutations of A}, S stands for symmetric. Later used in Symmetric Group of A.
.
M(A) = {all mappings of A to A}
Composition is an associative binary operation on M(A).
Identity map.
S(A) is closed under
So S(A) has an identity
S(A) = symmetric group of A.
Lemma:
Proofs, in book. Lemma 1.24, 1.25, 1.26
1. 6 Matrices (skipped, pre-req)
1.7 Relations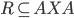
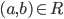
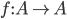is a binary relation on A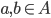
A binary relation on a set A is a subset
Usual notation is we write a R b if
A function
(a, f(a))
Ex: Universal relation all pairs in A X A
(a,b) all
02/17/2016
A X A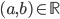
.
A is a set
A binary relation R on A is a subset R
We often put R in the middle aRb if
Def: A binary relation R is an equivalence relation if
1). R is reflexive: aRa for all a in A.
2). R is symmetric: aRb implies bRa for all a,b in A.
3). R is transitive: aRb and bRc, then aRc for all a,b,c in A
Notation: If R is a equivalence relation on A, and a in A, then
[a] = {b in A, s.t. bRa}
is called the equivalence class of a. "team of a".
Example: R is equivalence modulo 2
[0] = evens
[1] = odds
example: aRb if |a| = |b|
[0] = {0}
[x] = {x,-x} if x != 0.
Theorem: If R is an equivalence relation on a non-empty set A, then the equivalence classes form a partition of A.
[b] = {}
[b] != {}, then [a] = [b]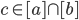
, want [a] = [b]
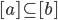and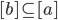 
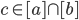
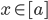, want 
,
.
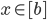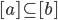
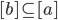Proof:
Need the equivalence classes are non-empty, pairwise disjoint and exhaust A (each a in A is in some equivalence class).
1). If a in A, then [a] != {} because aRa by reflexive.
2). a in [a], the equivalence classes exhaust A.
3). if [a] != [b] what [a]
We prove contrapositive,
we prove if [a]
Let
Need
means cRa and cRb
let
so, xRa, by symmetry aRc, so xRa and aRc, so xRc by transitivity.
Since xRc and cRb, we get xRb by transitivity.
So, x in [b]
thus,
Switching all a's and b's shows
So [a] = [b].
Thus the equivalence classes give a partition.
Chapter 2: Integers
skipping 2.1
Induction
1. base case (P_1 is true),
2. assume P_n is true, then P_n+1 is true.
Strong Induction (book calls it complete induction)
1. base case P_a is true
2. Induction step: assume P_k is true for all a <= k < n.
Example: A natural number p>1 is prime if p = mk with m,k in positive integers, then m=1 or k=1.
If n>1 is not prime, then n is composite.
Prop: Every number n>1 can be expressed as a product of primes.
Proof:
Base case, n=2.
Inductive hypothesis: Assume if 2 <= k < n, then k is a product of primes.
want n is a product of primes.
Case 1: n is prime
then n is a product of 1 prime. Good.
Case 2: n is composite
Then n = mk where 1 < m, k' < n
By induction m = p_1...p_s; k' = q_1...q_r,
where p_1,...,p_s, q_1,...,q_r are primes.
Then n = mk' = p_1...p_s(q_1...q_r) is a product of primes.
Example: Towers of Hanoi.
02/22/2016
Homework 2 is due Monday Feb 29.
1.5: 6,8
1.6: 8, 10,
1.7: 4, 10,
2.2: 8,10
2.3: 12, 24
2.4: 4,10,12,20
Test 1 is March 2
2.3 Divisibility
Well Ordering Principle
If S is a non-empty set of positive integers, then S has a least element.
Well Ordering Principle is equivalent to induction
Example: 7|9^n-2^n for all n \geq 1.
Proof by induction:
Base: n = 1, etc...
Assume 7|9^n-2^n
Want 7|9^{n+1}-2^{n+1}
9^{n+1}-2^{n+1} = 9(9^n-2) + 2^n(9-2) = 9(9^n-2) + 7(2^n)
By inductive hypothesis
7|9^n-2^n
So 9^n-2^n = 7C, C in Z
9^{n+1}-2^{n+1} = 9(7(C)) + 2^n(7) = 7(9C+2^n)
So 7|9^{n+1} - C^{n+1}
So, 7|9^n-2^n for all n \geq 1, by induction.
Proposition: The only divisors of 1 are \pm 1
Theorem(Division Algorithm)
Let a,b in Z with b > 0.
Then, \exists a unique q in Z, and 0 \leq r < b such that a = bq + r.
q is called quotient and r is the remainder.
Proof:
Uniqueness of q
Assume
1: a=bq_1 + r_1
2: a=bq_2 + r_2
Where 0 \leq r_1, r_2 < b
Assume r_1 \leq r_2
Then subtract equation (1) from equation (2):
0 = b(q_2 - q_1) + r_2 - r_1
so, r_2 - r_1 = b(q_1-q_2)
Case 1: q_1 - q_2 = 0
Then q_1 = q_2 and r_2 - r_1 = 0
So, r_2 = r_1.
Case 2: q_1 - q_2 != 0. Then since
b > 0 and r_2-r_1 > 0 => q_1 - q_2 > 0 => q_1 - q_2 >= 1.
So, r_2 >= r_2 - r_1 = b(q_1 - q_2) >= b
This contradicts r_2 < b. So case 2 doesn't happen. So, q_1 = q_2 and r_1 = r_2 in all cases. Existence: We first show if a>=0, b>0, then
a = bq + r with 0 <= r < b
We prove this by induction on a.
Base case, a = 0.
0= b(8) + 0
q=0, v=0.
We win.
We assume true for 0 \leq k < a
Case 1: a < b
a = b(0) + a
and 0 \leq a < b
Case 2: a >= b
Then a-b >= 0, and a-b < a
So a - b = bq' + r with 0 \leq r < b
So a = b + bq' + r = b(1+q')+r, 0 \leq r < b
So q = 1+q'
r = r.
This does a >= 0.
If a &t; -,
then -a > 0,
so by previous case
-a = bq + r with 0 \leq r < b
So = a = b(-q) + (-r)
Case 1: r = 0
then a = b(-q) + 0
So done.
Case 2: 0 < r < b
then a = b(-q-1) + b-r
and 0 < b-r < b
so b-r is the remainder.
2.4 Prime Factors and GCD
Theorem: let a, b be integers not both zero. Then, a, b have a unique gcd d.
Moreover, d is the smallest positive integer that can be written in the form d = ma + nb with n, n in Z.
Proof: uniqueness
if d_1, d_2 are GCDs of a and b, then
1: d_1 > 0, d_2 > 0
2+3: d_1 | d_2 (take c = d_1)
and d_2 | d_1 (take c = d_2)
So, d_1 = xd_2, d_2 = yd_1, (x, y > 0)
So, d_2 = y(xd_2) = yxd_2
So 1 = yx and x, y > 0
So x = 1 = y
So d_1 = d_2.
Existence: Let S = {m in Z^+ | m = xa + yb for some x, y in Z}
Is S empty? no.
a, -a, b, -b, and one of them has to be positive. And not both a and b are 0.
Let d be least element of S
Claim: d is gcd of a,b
1. d > 0, yes. S only has positive integers.
2. Need d|a and d|b
By division algorithm,
a = dq + r where 0 \leq r < d
Want r = 0.
r = a - dq
Since d \in S
then d = xa + yb with x, y \in Z
So, r = a - (xa + yb) q = (1-xq)a - yqb
if r > 0, then r \in S, but r < d,
So this contradicts d is the smallest in S.
So r must be 0, then a = dq so d|a. Similarly, d|b
3. Need if c|a and c|b, then c|d.
Well d = xa + yb
since c|a, c|b => a = mc and b = nc
So d = xmc + ync
= c(xm+yn)
So, c|d, therefore, d is gcd.
QED
Notation: The book writes (a,b) for the GCD of a and b.
Prof likes gcd(a,b).
How to compute GCD
Euclidian algorithm (related to Lame theorem)
02/24/2016
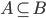: If n is a common divisor of c, d, then c=nx and d=ny.
Review: GCD(1717,1111)
Why it works:
gcd(a,b) = gcd(b,r) = gcd(r1, r2)...
Lemma:
If c = dq + r, then gcd(c,d) = gcd(d,r)
Proof:
let A = {common divisors of c,d}
let B = {common divisors of d,r}
Claim: A = B
So, nx = nyq + r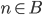
, so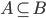 
.
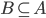
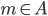, thus A = B
r = nx - nyq = n(x-yq)
so, n|r
Also n|d, since d=ny
thus
Want
Let m be a common divisors of d and r. Then d = mx, r = my
So, c = dq + r = mxq + my = m(xq + y)
So, m|c, also m|d
So,
QED
Two integers a,b are relatively prime if gcd(a,b) = 1
Theorem (2.14): If a, b are relatively prime and a|bc, then a|c
Proof: By assumption gcd(a,b) = 1
write 1 = am + bn with m, n
Multiply both sides by c
c = amc + bcn
By assumption bc = ax, some x in Z
c = amc + axn = a(mc+xn)
so, a divides c.
Cor: If p is a prime and p|ab, then p|a or p|b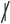
a.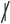
a. So, a, p are relatively prime.
pf: Suppose p
Then gcd(a,p) = 1 since p only has divisors 1,p and p
Thus, p|b by the theorem.
Cor 2.17: If p is prime and p|a_1...a_n, then p|a_i for some i.
Pf: This is a nice exercise in induction.
Fundamental theorem of Arithmetic
Each integer n > 1 can be uniquely expressed as a product of (positive) primes up tot he order you write the product.
Proof: We already saw that each number n > 1 can be expressed as a product of primes. We just need uniqueness.
Assume p_1...P_r = q_1...q_s
where p's and q's are primes.
Want r = s. And after reordering the primes are the same on both sides.
We prove this by induction on r.
Base case: r = 1
then p_1 = q_1...q_s
Since p, is prime, we must have s = 1, so p_1 = q_1.
Assume true for r and let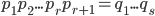
Note p_{r+1} | q_1...q_s
by the corollary p_{r+1} divides some q_i.
By reordering q_1 ...q_s we may assume p_{r+1}|q_s
Since q_s is prime and p_{r+1} \neq 1 \Rightarrow p_{r+1} = q_s
And so p_1...p_rp_{r+1} = q_1...q_{s=1}q_{r+1}
So, p_1...p_r = q_1...q_{s-1}
By induction, s-1 = r, that is, s = r+1.
and p_1,...,p_r is q_1,...,q_{s-1} up to reordering
So, s = r+1 and q_1, ..., q_s
is a reordering of p_1, ..., p_{r+1} QED
Warning: Factoring a number into primes in reasonable time is beyond current human comprehension.
LCM: Least common multiple
An lcm of two integers a, b != 0, is an integer m s.t.
1) m > 0
2) a |m and b|m
3) if a|c and b|c => m|c
Fact: lcm(a,b) = ab/gcd(a,b)
Euclid Theorem
There are infinitely many primes.
End of 2.4
Test 1 stops here
2.5 Congruence Mod n
Equivalence class of a
[a] = {a+nk | k \in Z}
This is called the residue class of a mod n.
Ex: The residue class of 0 modulo 2:
[0]=even, [1]=odd={1+2k| k in Z}
Pro: If m \in Z and m = nq + r with n: 0 <= r < n
r (mod n)
r (mod n)
Then m
pf: m - r = nq a multiple
so m
So, two guys are equivalent mod n if they have the same remainder when you divide by n.
So each equivalence class of mod n is of the form: [0], [1], ..., [n-1].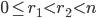
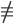r_2 (mod n)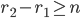
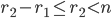
Note if
then r_1
Note if 0 < r_2 - r_1 = qn
then q > 0, so
But
Morale:
[0],[1],...,[n-1] are distinct equivalence classes.
02/29/2016
Test: Except 2.1
Format:
Multiple-multiple choice
Long answers approx. 4-5
1. One set theory proof
2. Induction or GCD style proof
3. Euclidean alg. with back sum.
Theorem 2.22, Proposition: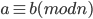
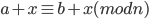
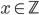
If
then:
ax = bx (mod n)
for all
Proof: So n|a-b
b+x (mod n)
so, a-b = dn
(a+x) - (b+x) = a-b = dn
So, n |(a+x) - (b+x)
so, a+x
ax - bx = (a-b)x = dnx
bx (mod n)
So, n|ax - bx
S, ax
QED
Theorem 2.23: Substitution Property:
Suppose aΞb (mod n) and cΞd (mod n)
Then, a + c Ξ b + d (mod n)
ac Ξ bd (mod n)
Proof:
1). a+c Ξ b+c (mod n)
by the proposition with x = c
b+c Ξ b+d (mod n), by prop.
So, a+c Ξ b+d (mod n) by transitivity
2). ac Ξ bc (mod n)
by prop with x = c
Also, bc Ξ bd (mod n) by prop.
So, ac Ξ bd (mod n)
by transitivity.
Example: Prove
7 | 9^n - 2^n, for all n >= 1.
9Ξ2 (mod 7)
9x9 Ξ 2.2 (mod 7)
9^n Ξ 2^n (mod 7) for all n >= 1
So, 9^n - 2^n Ξ 0 (mod n)
So 7 | 9^n - 2^n
QED
Example: prove n(n+1) is even for all n >= 1.
If n Ξ 0 (mod 2)
n+1 Ξ 1 (mod 2)
n(n+1) Ξ 0(1) mod 2)
Ξ 0 mod 2
If nΞ1 (mod 2), then n+1 Ξ 0 (mod 2)
n(n+1) Ξ 1(0) (mod 2)
Ξ 0 (mod 2)
QED.
Weird stuff:
2.2 Ξ 0 (mod 4)
Fun stuff:
A number n is divisible by 5 IFF its last digit is 0 or 5.
General notation:
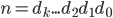, decimal expansion
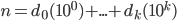
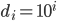place digit.
A number is divisible by 4 if the last 2 digits are divisible by 4.
10Ξ2 (mod 4)
10^2 Ξ 2^2 (mod 4)
Ξ 0 (mod 4)
10^3 Ξ 10(10^2) (mod 4)
Ξ 10(0) (mod 4)
Ξ 0 (mod 4)
10^k Ξ 0 (mod 4), for k >= 2.
So, if n has decimal expansion
n Ξ d_0+d_1(10) (mod 4)
so, n Ξ last 2 digits (mod 4)
example: 2105326 Ξ 26 (mod 4)
Casting out nines:
n is divisible by 9, if sum of digits is divisible by 9.
Example: 13020201 is divisible by 9
So, 3 divides a number if it divides sum of digits.
n Ξ sum of digits (mod 3)
So, n Ξ last 3 digits (mod 8)
Divisibility by 11:
Any even length palindrome number is divisible by 11.
Proof:
10Ξ -1 (mod 11)
100 Ξ 1 (mod 11)
So, if n has decimal expansion,
n Ξ d_0 + ... (mod 11)
So, n Ξ alternating sum of digits starting at ones place (mod 11)
Theorem 2.24: Cancellation Law:
If a and n have a common divisor. You cannot always cancel a in:
ax Ξ ay (mod n)
Proven
Theorem 2.25: Linear Congruences
If gcd(a, n) = 1, then
the congruence ax Ξ b (mod n) has a solution integer x and any two solutions are congruent mod n.
Example:
solve 37x Ξ 2 (mod 39)
check gcd(37,39) = 1
step: write 1 as a linear combo of 37, 39
39 = 1(37) + 2
37 = 18(2) + 1
18 = 18(1) + 0
Back sub:
1 = 37 - 18(2)
= 37 - 18(39-37)
= -18(39) + 19(37)
Take both sides mod 39
1 Ξ 19.37 (mod 39)
since 39 Ξ 0 (mod 39)
2 Ξ 2(19)(37) (mod 39)
x = 2(19) = 38
2 Ξ 37（38) (mod 39)
03/07/2016
Theorem 2.26 with proof.
Ex: solve 5x\equiv 7 (mod 21)
21 = 5*4 + 1
1 = 21 - 5*4
1\equiv 5(-4) (mod 21)
7\equiv 5(-4)*7 (mod 21)
7\equiv 5(-28)(mod 21)
x = -28
x=14 also works, since 14\equiv -28 (mod 21)
Theorem 2.28 Chinese Remainder Theorem
Let gcd(m,n) = 1, and a, b in Z, then there exists x in Z.
x\equiv a (mod m)
x\equiv b (mod n)
Any two solutions are congruent mod mn.
(a little different than book)
Proof: Write
(*)1 = rm+sn with r, s in Z
Crossing trick:
x = brm + asn
Claim: x works
1 \equiv sn (mod m)
1 \equiv rm (mod n)
since m|rm and n|sn by (*)
x \equiv a (mod m)
since brm \equiv 0 (mod m)
a(sn) \equiv a(1) (mod m)
\equiv a (mod m)
x = brm + asn \equiv a (mod m)
x \equiv b (mod n) since
asn \equiv 0 (mod n)
brm \equiv b(1) (mod n)
x = brm + asn \equiv b (mod n)
So, x is a solution
Uniqueness:
If x \equiv a (mod m)
x \equiv b (mod n)
y \equiv a (mod m)
y \equiv b (mod n)
x \equiv y (mod m)
x \equiv y (mod n)
So, m|x-y, n|x-y
So, mn = lcm(m,n) | x-y
(note gcd(m,n) = 1 means lcm(m,n) = mn)
So, x \equiv y (mod mn)
Example:
x \equiv 3 (mod 6)
x \equiv 4 (mod 7)
Solution:
The method
7 = 6+1
1 = 7-6
Crossing method
x = 3*7 - 4*6
= 21 - 24 = -3
So, x \equiv 39 (mod 42)
39 \equiv 3 (mod 6)
39 \equiv 4 (mod 7)
Yes, it worked.
Example, solve:
x \equiv 2 (mod 41)
x \equiv 7 (mod 121)
Solution:
Euclidian method:
121 = 41*2 + 39
41 = 39 + 2
39 = 2*19 + 1
Thus, 1 = 20(121) - 59(41)
Crossing trick:
x = 20(121)(2) - 59(41)(7) = -12,093
41(121) = 4961
-12,093 \equiv 2790 (mod 4961)
x = 2790
Chinese Remainder Theorem vs. 2.0, theorem 2.28
Just like the book
2.6 Congruence Classes
Zn = {[0],[1],...,[n-1]}
= set of congruence classes mod n
Z_2 = {[0],[1]}
Z_3 = {[0],[1],[2]} = {[1],[2],[3]}
Theorem 2.29 Addition in Zn
Proven partly by substitution principle
Example 1 of book used for theorem 2.30 Multiplication in Zn: [a][b] = [ab]
Theorem: Mult mod n is assoc, comm, has identity [1]
03/09/2016
Sec. 2.6, 2.8
Continue RSA cryptography:
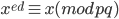
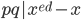
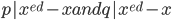
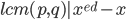
Key exchange:
Your computer uses RSA to send the bank a symmetric key code.
Question:
why can Bob decode by
Want:
want :
want
since lcm(p,q) = pq as p,q are prime
want:
Then
Fermat's little theorem: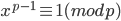
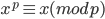, for all x.
if p is a prime and p+m, then
Alternate version:
W will prove this in one line in chapter 3.
Recall: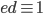
(mod (p-1)(q-1))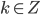
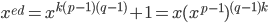
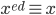(mod p)
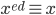(mod q)
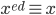(mod pq)
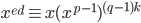(mod p)
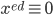(mod p)
(mod p) done.
ed-1 = k(p-1)(q-1) for some
ed = k(p-1)(q-1) + 1
want
and
If so
by squared expression on other board,
if p|x,
Else if p does not divide x,
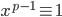(mod p) by Fermat
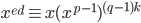(mod p)
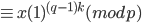
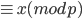
so
Same computation works for q.
So, x^{ed} \equiv x(x^{p-1})^{(q-1)k} (mod q)
by Fermat's little thm. for q
So x^{ed} mod m = x
so it works.
Silly example:
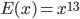mod 77, encryption
1(mod 60)
-23(13) (mod 60)
37 (mod 6)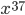
mod 77
p = 7, q = 11, m = 77, (p-1)(q-1) = 60
e = 13
Need d with
ed
1 = 5(60) - 23(13)
So 1
-23
D(x) =
03/14/16
Happy Pi day
Chapter 3
HW 3 is due Wed. March 16.
2.5: 22,32,34,56b,e
2.6: 6c, 10e,f, 22 (Hint: if x^2 is congruent to 1 (mod p), then p divides x^2-1. Now factor.
2.8: 8,22
3.1 4,26,32
===
A group is a set G with binary operation * : G X G -> G s.t.
1) * is associative
2) G has an identity
3) Each element of G has an inverse
G is called an abelian group or commutative group if x*y =y*x, for all x, y in G
Example:
(Z, +) is a group
Other groups: (R,+), R-{0},.), (R^+,.), (Q-{0},.), (R^n,+),({1,-1},.), some tables, (Z_n,+)
Example:
A is a set, S(A) = group of permutation of A is a group with binary op. composition of functions.
Example:
{1,i,-i,-1} are a group with mult.
Example: Klein 4-group
Binary operation matrix mult.
Def: The number of elements of a group is called its order. |G| = O(G) for the order of G.
Thm: let G be a group (Theorem 3.4)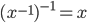
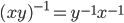
a. The identity of G is unique
b. Inverses are unique
c.
d.
e. Cancellation law:
- xy = xz => y=z
- yx = zx => y=z
Proven
Exponents: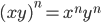
by induction.
If G is a group and a in G, we "Define" for n>0, a^n = a....n times...a
Def 3.8 Integral Exponents
Theorem 3.9 Laws of Exp.
Proven: If G is abelian
For abelian groups we often write binary op as + and use 0 for identity and -x for the inverse of x.
This is called additive notation.
a + ...n times... + a = na
In general, for additive notation, we write na instead of a^n for n in Z.
Laws of exp. become laws of multiples
Theorem 3.9
Example: Let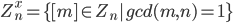
Then Z^x_n is a group with respect to mult.
Recall: Z^x_n is the set of guys with mult. inverses mod n.
Example: Z^x_2 = {[1]}
Z^x_3 = {[1],[2]}
Z^x_4 = {[1],[3]}
Z^x_5 = {[1],[2],[3],[4]}
Section 3.3 Subgroups
Prop: Z(G) is a subgroup of G = Theorem 3.14
Proof: We need closure under properties 1,2,3:
1.) Identity: Is e in Z(G)?, if x is in G, then xe = x = ex, so e in Z(G)
2.) Closed under binary op.
assume g1, g2 in Z(G), we want g1g2 in Z(G).
Since g1 in Z(G), g1(x) = x(g1), for all x in G
Same with g2.
Want: g1g2(x) = x(g1)(g2) for all x in G
Let's test: If x in G,
x(g1)(g2) = g1(x)(g2) = g1(g2)(x)
Since x was arbitrary, g1g2 in Z(G)
3.) Closure under inverse: g in Z(G) => g^{-1} in Z(G)
Since g in Z(G), xg = gx, for all x in G
Want: g^{-1}x = xg^{-1} for all x in G
Multiply xg=gx on the left and right by g^{-1}.
So, g^{-1} \in Z(G)
Thus, Z(G) is a subgroup of G
Example of G = 2x2 invertible real matrices, center of G:
Z(G) = {[a 0\\0 a] | a != 0}
Example: Trivial subgroup {e} of any group G.
Silly example: G is a subgroup of G.
03/16/2016
Def: Let G be a group let a in G, then <a> = {a^n | n in Z}
This is a subgroup of G called the cyclic subgroup generated by a
Ex: G = C -{0} under mult.
<i> = {1,i,-1,-i}
invertible 2x2 matrices over R
(Z_12,+), <[8]> = {[0],[8],[4]}
G is cyclic group if G = <b> for some b in G. The element b is called a generator.
Generators don't have to be unique.
For additive groups (G,+), <a> = {na | n in Z}
Example: Z with +
Z = <1> = m(1) | m in Z}
= <-1>, So Z is an infinite cyclic group.
G = {e}, G = <e> is cyclic
Z_n = <[1]> = {m[1] | m in Z} = {[m] | m in Z}, Z_n is a cyclic group.
Example: {1,i,-1,-i} with mult. = <i>, <-i>.
Example: Z_10, <[3]> = {[0], [3], ..., [7]} = Z_10. So [3] is a generator.
Example: Klein 4 group: This is not cyclic. <e> = {e}, <a> = {e,a} since a^2 = e, ... none of all 4 are generators.
Prop: Cyclic groups are abelian.
Proof. If G is cyclic, then G = {a^n | n in Z}
let g, h in G. Need gh = hg
Exists k, m in Z, s.t. g = a^k, h = a^m,
so gh = a^ka^m = a^{k+m} = a^{m+k} = a^ma^k = hg
So G is commutative. QED
Example: Z^x_7 x is relative prime to 7, with mult. = {[1],...,[6]}
<[3]> = {[1],[3],[2],[6],[4], [5]}, [3]^0, [3]^1, ...
This is true for any prime.
I got busy...find recording to continue.
03/21/2016
HW 4 is due Wed, March 30:
3.2: 8,15, 18, 20a
3.3: 4,8,10,15b,19b,20
3.4: 6,8, 10a,d, 21,24
Note that 3.4 will be covered in Monday's class.
Review Cyclic Group
If a \in G, either:
1) all powers of a are distinct, or
2) a^n = e for some n >= 1
Theorem If n>=1 is the least positive integer with a^n = e, then:
i) <a> = {e, a, a^2, ..., a^{n-1}}
ii) a^s = a^t \Leftrightarrow s \equiv t (mod n)
Def: If a \in G, then the order of a, denoted |a| or O(a), is the size/order of <a>.
Find matrices example, I copied to notebook.
Example:
Z^x_5 = {[1],[2],[3],[4]} with x (times/multiplication)
O([2]) = 4
[2]^1 = [2]
[2]^2 = [4]
[2]^3 = [3]
[2]^4 = [1]
Z^x_5 = <[2]>
Theorem 3.24, with proof (use gcd theorem).
Example:
If a,b in Z, neither are zero
G = Z = <1> with +
H = {ma + nb | m,n in Z}
I promise H = <d> where d is the least positive integer with d in H. i.e. ≪gcd(a,b)>
Theorem 3.26, proof shown
Example: G = Z_{12}, + = <[1]>
Possible subgroups are <[1]>,<[2]>,<[3]>,<[1]>,<[6]>,<[12]> = <[0]>
<[9]>=<[3]> Since gcd(9,12) = 3
Theorem says for Z_n with + and a = [1]
<[m]> = <[d]>
d = gcd(m,n)
Example: Z_{138},+
<[11]> = <[1]> = Z_{138}
gcd(11,138) = 1
Theorem 3.28 Proof given
List all generators of Z_{12} with +,
ince Z_{12} = <[1]>
generators are [m] s.t. gcd(m,12) = 1
[1],[5],[7],[11]
03/28/2016
Review: Theorem G = <a> finite cyclic group of order n.
Then <a^m> = <a^d>
where d = gcd(m,n)
Cor: |a^m| = n/d
Pf: |a^m| = # of elements in <a^m>
= # of elements in &a^d> = least positive k s.t. (a^d)^k = e
d(n/d) = n
so (a^d)^{n/d} = a^n = e
So order a^d is at most n/d
If 1 \leq k < n/d, (a^d)^k = a^{dk}
and dk < d(n/d) = n
So, a^{dk} != e
Since n is least positive integer with a^n = e
Cor: <a^n> = <a>, IFF gcd(m,n) = 1
pf: Since n/gcd(m,n) = |a^m|
So |a^m| = n \Leftrightarrow gcd(m.n) = 1
Example: Z_12 = <[1]> under +
ans: <[10]> = <[gcd(10,12)]> = <[2]>
|[10]| = 12/2 = 6
Example: Z_60 generated by [36]
|[36]| = 60/gcd(36,60)
<[36]> = <[12]> = 60/12 = 5
In Z_n, +
<[m]> = <[gcd(m,n)]>
|[m]| = n/gcd(m,n)
-----------------
List all generators to Z_20
{[m] | gcd(m,20) = 1, 0 \leq m \leq 19}
[1],[3],[7],[9],[11],[13],[17],[19]
(possible exam question)
List all subgroups of Z_20, assuming for +, with no repetitions
divisors of 20:1,2,4,5,10,20
Here [] means <[]>
[20]=[0] \subset [4] \subset [2] \subset <[1]>
[10] \subset [2]
[0] \subset [10] \subset [5] \subset [1]
W = cos(2pi/n) + isin(2pi/n)
W^k = cos(2pik/n) + isin(2pik/n)
W^n = 1
<W> = \{1,w,w^2,...,w^{n-1}\} is a cyclic group of order n.
W^m is a generator when gcd(m,n) = 1
The w^m with gcd(m,n) = 1 are called primitive nth-roots of unity.
6th root of unity
W, W^5 are primitive 6th-roots.
graph drawn:
W_1 through W^5 plotted throughout 2D graph evenly around counterclockwise.
===========
3.5 Isomorphisms
Example 2 shown
Definition 3.29
Example: f:Z^+_12 -> {F,T}^{XOR}
f([0]) = F
f([1]) = T
is an isomorphism
Example:
Z_4,+, {1,i,-1,-i}
f([m]) = i^m gives an isomorphism f:Z_4 -> {1,i,-1,-i}
Example: G = R with +
H = positive reals with
f:G->H
f(x) = e^x
f(x+y) = e^{x+y} = e^xe^y = f(x)f(y)
Is Z4,+ is isomorphic to Z_6,+? No
There is no bijection from Z_4 to Z_6
Example:
Is Z^+_4 isomorphic to Klein 4 group? No. Tables drawn to clarify. e is diagonal in Klein 4 table while there's none such pattern in Z_4.
Theorem 3.30
add c) to theorem:
c). f(x^n) = f(x)^n for all n in Z
04/04/2016
Test #2 format:
1 question on divisibility rules (2.4 or 2.5?)
11 multiple choice
5 long answers
2 proofs, the others computational
No crypto.
Test 2 on Wed covers
2.5 (starting from solving linear congruences), 2.6, 3.1, 3.2, 3.3, 3.4, 3.5 and one question on divisibility rules.
Some suggested problems on isomorphism 3.5: 2a,3,9,10,17
Format is again multiple-multiple choice and long answers. Be prepared to solve linear congruences, solve systems of linear congruences (chinese remainder theorem), prove stuff about groups and prove stuff about divisibility. Know your cyclic group stuff.
3.6 Homomorphisms
Let G be a group with binary op *
and H a group with binary op @
A homomorphism from G to H is a map f: G-> H
satisfying f(x*y) = f(x)@f(y)
Note an isomorphism = bijective homomorphism
Example: f: Z_4 -> Z_2 with +,
f([0]) = [0]
f([1]) = [1]
f([2]) = [0]
f([3]) = [1]
Uses 3 tables to show clarity: Z_4, Z_2, Z_2 with 2 more row&col.
Example: f: Z->Z_n
f(x) = [x]
is a hom.
f(x+y) = [x+y]
f(x) + f(y) = [x]+[y]
So f is a hom.
If f:G-> G is a hom.
the f is called an endomorphism
If f:G-> H is an onto hom.
f is an epimorphism
If f:G-> H is a 1 to 1 hom.
f is called monomorphism
If there exists an onto hom f:G-> H then H is called a homomorphic image of G.
Example: f:G->H
f(g) = e_H (identity of H) for all g in G
is a hom. called the trivial hom.
f(g_1 g_2) = e_H
f(g_1)f(g_2) = e_H e_H = e_H = f(g_1 g_2)
so f is a hom.
Prop: If f:G->H is an onto hom.
1. If G is abelian, then H is ablian
2. If G is cyclic, then H is cyclic
Proven.
Def. let f:G->H be a hom.
The kernel of f is Ker f = {x in G | f(x) = e_H}
(same kernel idea in vector space)
example: If f:G->H is the trivial hom. f(g) = e_H, for all g in G
Ker f = G
Example: f: Z->Z_n
f(x) = [x]
Ker f = {x in Z | f(x) = [0]} = multiples of n = n Z = {na | a in Z}
Example: If V, W are vector spaces and T:V->W is a linear transf.
So T is a hom. with respect to +.
Ker T = {v in V | T(v) = 0}
Prop: Ker f is a subgroup of G for a hom. f:G->H
(might be on test in future)
Proven
Prop: A hom. f: G-> H is 1-to-1 IFF Ker f = {e_G}
proven.
Thm: Let G be a cyclic group
1. If |G| = infinity, then G iso to Z
2. If |G| = n < infinity, then G iso to Z_n
Proven.
Chapter 4: Finite Permutation groups
04/11/2016
Test 2: mean 83, median 86
2-Cycle = transposition
Definition
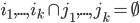
Cycles (i_1,...,i_r) and (j_1,...,j_k) are disjoint if
Fact: Disjoint cycles commute
Goal: To show every permutation is a product of disjoint cycles
Fact: Every permutation in S_n is a composition of transpositions
Proof:
It's enough to do it for a cycle since each permutation is a product of a cycles.
(i_1,...,i_r) = (i_1,i_2)...(i_{r-1}, i_r}
r-1 transpositions
Typical exam question:
Example: f = (1 2 3 4 5 6 7 8 9 || 2 4 6 8 1 9 5 7 3)
"||" is used for newline indication
write f as a product of transpositions
Step 1: Write as disjoint cycles
f = (1,2,4,8,7,5)(3,6,9)
Step 2: break the cycles into transpositions
f = (1,2)(2,4)(4,8)(8,7)(7,5)(3,6)(6,9)
Even & odd permutations
Determinants
If you permute the rows of a matrix then if your permutation is a product of an even # or transpositions the determinant does not change. If your permutation is a product of an odd # of transpositions, the determinant changes sign.
Conclusion:
A permutation cannot both be a product of an aeven number of transpositions and an odd number of transpositions.
Def: A permutation f in S_n is even if it can be written as a product of an even number of transpositions;
A permutation f in S_n is odd if it can be written as a product of an odd number of transpositions.
Example: f = (1,2,3) is even = (1,2)(2,3)
An r-cycle is odd IFF r is even
Example: f = (1,3,7,2)(4,6,8)(1,2,3,4,5) is odd
Let A_n = {f\in S_n | r is even} = all even permutations of {1,...,n}
A_n is a subgroup of S_n called the alternating group.
= a product of 2k + 2m transp.
Proof:
Id = product of O transpositions
If f is a product of 2k transp.
g i s a product 2m transp.
so
If
since (i,j)^{-1} = (i,j)
So
Example: Game of 15
4x4 numbered squares, if permutation is odd, cannot solve.
You cannot solve an odd perm with blank in the lower right corner.
Black is in an E square on an even move and an O suqare in an odd move
So to get blank back to lower right corner you need an even number of moves.
Each move is a transposition so you cannot solve it if the initial config is an odd perm with blank in an even position.
04/13/2016
Homework 5 is due Wed, April 20.
3.5: 2a,3,9,10,17,
3.6: 4, 6, 11, 12
4.1: 1d,h, 2a,b,c,d,f, 4a,b,c,d,f, 5d,h 6a,b,c,d,f, g,h, 8d,f,10d,13d
Conjugacy
are conjugate if
with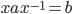 
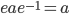
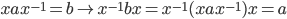
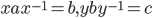
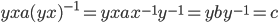
If G is a group,
Being conjugate is an equivalence relation on G:
Reflexive:
symmetric:
Transitive:
Pf by induction, try.
Example:
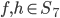
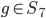, with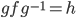 
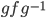= (g(1),g(3),g(7),g(2)) = (4,6,3,5) = h
f = (1,3,7,2)
h = (4,6,3,5)
Find
g = (1,4)(2,5)(3,6,7)
check with
What if you don't have a cycle
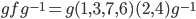
Example: f=(1,3,7,6)(2,4)
=(g(1,3,7,6)g^{-1}(g(2,4)g^{-1})
=(g(1),g(3),g(7),g(6))(g(2),g(4))
Example:
f = (1,3,7,6)(2,4)
h = (3,4,7,2)(5,1)
find g \in S_7 with gfg^{-1} = h
g = (1 2 3 4 5 6 7 \\ 3 5 4 1 6 2 7)
Example: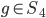
with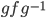 
= h and if so find it?
f = (1,2)(3,4)
h = (1,3,2,4)
Is there
There is none, because h is not a product of 2 disjoint cycles.
Example:
with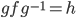 
f = (3,1,2,5)(6,8)(10,9,4)
h = (1,3,7,6)(2,8,5)(4,10)
Find
or explain why there is none.
h = (1,3,7,6)(4,10)(2,8,5)
g = (1 2 3 4 5 6 7 8 9 10 \\ 3 7 1 5 6 4 9 10 8 2)
Theorem: Two elements of S_n are conjugate if and only if their disjoint cycle decompositions have the same number of cycles of each length.
Order of a permutation
f = (1,3,4)(2,11,5)(8,9)
What is the order of f?
Theorem: Order of f \in S_n
is lcm of the lengths of the cycles in its disjoint cycle decomposition
Example what is the order of
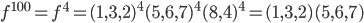
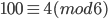
f = (3,7,2,5)(1,6)(8,10)
order of f = 4
f = (1,3,2)(5,6,7)(8,4)
(8,4)^4 disappears because it is identity since order of it is 2, raised to power 4.
Cayley's Theorem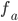
is a permutation, 
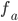is 1 to 1, fa is onto
Every group G is isomorphic to a group of permutations that is a subgroup S(A) for some set A.
Proof:
Claim 1:
Define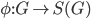
is 1 to 1
Claim A: \phi is a homomorphism
Claim B:
check ker
Szies: each subgroup has size dividing 30.
is a subgroup, then |H| divides |G|.
LaGrange's Theorem
If G is a finite group and
Fermat's little theorem (used last time in cryptography)
mod p
mod p)
with multiplication.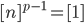
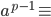(1 mod p)
if p is prime
pf: If p|a, then duh. (
Assume gcd(a,p) = 1
We will show
Then multiply both sides by a.
Let
This is a group with p-1
Consider H = < [a]> under mult.
then |H| divides |G| = p-1.
So order of [a] with respect to mult divides p-1.
So
So
My Own:
I've been trying to figure out the connection between Associativity and Commutativity.
Commutative does not imply associative. e.g. f(x,y) = xy+1
As for associativity, I think it has to do with symmetric as a whole (the while definition of the operation, such as the above example);
while commutativity has to do with symmetric only between the two variables (in binary operations).
04/18/2016 (Be sure to digest this entry)
Cor (from Lagrange theorem):
Let G be a finite group of order n, then a^n = e for all e in G
Pf:
let H = < a>
then |H| = o(a)
But |H| devides |G| = n
so o(a) | n implies a^n = e since n\equiv 0 (mod o(a))
Cor: Fermat's little thm:
a^p \equiv a (mod p) if p is prime
Pf:
If a \equiv a (mod p) duh
If gcd(a,p) = 1
then let G = Z_p - {[0]} under mult.
By corollary above
[a]^{p-1} = [1] since |G| = p-1
implies [a]^p = [a]
so a^p \equiv a (mod p)
Def: If n \geq 2
then \psi (n) = # \{m | 1 \leq m < n, gcd(m,n) = 1\}
Example:
\psi(2) = 1
\psi(3) = 2
\psi(4) = 2
\psi(5) = 4
\psi(6) = 2
\psi(p) = p-1, p = prime
Major fact: \psi(mn) = \psi(m)\psi(n) if gcd (mn) = 1
example: \psi (pq) = (p-1)(q-1), p,q prime
\psi(n) = # elements of Z_n with multiplicative inverses = |Z^*_n| = |U_n|
Z^*_n = \{[m]|gcd(m,n) = 1\} in Z_n with mult.
Euler's Theorem
If gcd(a,n) = 1
then a^{\phi(n)} \equiv 1 (mod n)
Note if p is prime a^{\psi(p)} = a^{p-1}
So this says a^{p-1} \equiv 1 (mod p)
if p \not| a
= Fermat's little theorem
Pf: If gcd(a,n) = 1 implies [a] = Z^*_n
Z^*_n is a group under mult of size |Z^*_n| = \psi (n)
So [a]^{\psi(n)} = [1] by corollary to Lagrange
So a^{\psi(n)} \equiv 1 (mod n)
Cor. If G is a group of prime order p, then G is cyclic and isomorphic to Z_p
Pf:
Let a \in G, a != e
Then | < a>| > 1
Since a!=e,
By Lagrange | < a>| divides |G| = p
Since p is prime, implies | < a> | = p,
since < a > \leq G
and | ≪ a> | = p = |G| implies < a> = G
So, G is cyclic, since all cyclic groups of order p are isomorphic to Z_p, done.
Pizza principle
Suppose a pizza with 6 slices, each with 2 pepperoni.
We cut G into slices each of which has |H| elements (pepperoni)
|G| = |H| x number slices
Motivation: X\equiv Y (mod n)
n | x-y
x-y = nk for k in Z
x-y \in nZ = {nk | k in Z}
nZ = < n> \subseteq Z
subgroup under +
Let G be a group and H \leq G for a,b in G
define a\equiv b (mod H)
b^{-1}a \in H
Example: G = Z,+
H = nZ = < n>
X \equiv y (mod nZ | x \equiv y (mod n)
Prop: \equiv (mod H) is an equiv. relation
Pf: Reflexive
a \equiv a (mod H)
a^{-1}a = e \in H
So, a \equiv a (mod H)
Symmetric:
a \equiv b (mod H)
Want b \equiv a (mod H)
b^{-1}a \in H since a \equiv b (mod H)
Want a^{-1}b \in H
a^{-1}b = (b^{-1}a)^{-1} \in H since H is closed under inverse.
So b \equiv a (mod H)
Transitive:
Assume a \equiv b (mod H), b \equiv c (mod H),
want a \equiv c (mod H)
c^{-1}b \in H since b \equiv c (mod H)
want: c^{-1}a \in H
So c^{-1}a = c^{-1}bb^{-1}a \in H
since H is closed under binary op.
So a \equiv c (mod H)
So \equiv (mod H) is an equiv relation. Done
Goal: Show each equivalence class has size |H|
If true |G| = |H| x # of classes.
Notation: If g \in G
then [g] is the equivalence class of g mod H
Recall [g] = \{x \in G | x \equiv g (mod H)\}
Prop: Let g \in G, H \leq G
1) [g] = \{gh | h \in H\} => notation: gH
2) |gH| = |H|
there is a bijection between H and G
Proof:
1). want \{gh \in H\} \subseteq [g]
let x \in \{gh | h \in H\}
So, x = gh with h \in H
Is x \equiv g (mod H)?
g^{=1}x = g^{-1}gh = h \in H, so x \equiv g (mod H)
=> x \in [g]
So, gH \subseteq [g]
Want [g] \subseteq gH = \{gh | h \in H\}
let x \in [g]
So x \equiv g (mod H)
so g^{-1} x \in H
let h = g^{-1} x \in H
then gh = gg^{-1}x = x
So [g] = gH = {gh | h \\in H}
2). Want a bijection \psi: H \rightarrow gH
\psi(h) = gh
one to one: Assume h_1, h_2 \in H
and \psi(h_1) =\psi(h_2), want h_1 = h_2
gh_1 = \psi(h_1) = \psi(h_2) \Rightarrow = h_1 = h_2 by cancellation
So \psi is 1 to 1.
Onto: let x \in gH
so x = gh with h \in H
x = \psi(h)
So \psi is onto
So \psi is bijection.
|gH| = |H|. Done
gH is called a left coset of H
the number of left cosets of H is called the index of H and is written [G:H]
Thm(Lagrange)
Let G be a finite group and H a subgroup. Then |G| = [G:H].|H|
and so size of H divides |G|.
So [G:H] = \frac{|G|}{|H|}
Proof:
Each equivalence class of \equiv (mod H) has |H| elements and there are [G:H] classes.
So |G| = [G:H].|H|
analogy: #pepperoni = #slices times #pepperoni per slice
Example: G = Z with +
H = 3Z = < 3>
List all cosets (will be on exam):
[0] = 0 + 3Z
note: gH for mult; g+H for groups with +
[1] = 1 + 3Z = {1+3k | k \in Z}
[2] = 2 + 3 Z = {2 + 3k | k \in Z}
[3] = 3 + 3Z = {3+3k | k \in Z} = {3(k+1) | k \in Z} = 0 + 3Z = [0]
[Z:3Z] = 3
Example: G = S_3
H = {e, (1,2,3), (1,3,2)} = < (1,2,3)> = A_3
[G:H] = \frac{|G|}{|H|} = \frac{|S_3|}{|A_3|} = 6/3 = 2
eH = {e, (1,2,3), (1,3,2)} = H
(1,2)H = {(1,2), (1,2)(1,2,3), (1,2)(1,3,2)} = {(1,2), (2,3), (1,3) }
two cosets only.
(1,3)H = (1,2)H
Example:
G = Z_{12}, +
H = < [3]> = {[0], [3], [6], [9]}
[G:H] = 12/4 = 3
list:
[0]+H = H = {[0], [3], [6], [9]}
[1]+H = {[1],[4],[7],[10]}
[2]+H = {[2],[5],[8],[11]}
Example:
G = S_n
H = A_n, even permutations
operation is composition
f is even if it is a product of an even number of permutations.
g is odd if it is a product of odd number transpositions.
eA_n = A_n = even permutations
(1,2) if f is odd
(1,2) \equiv f (mod A_n)
f^{-1}\circ (1,2) = odd.odd = even \in A_n
=> (1,2) \equiv f (mod A_n)
So, (1,2)A_n = all odd perms.
[S_n:A_n] = 2
|S_n| = [S_n:A_n].|A_n|
|S_n| = 2.|A_n|
So |A_n| = |S_n|/2 = n!/2
So half perms are odd and half are even.
04/20/2016
Recall:
a\equiv b (mod H)
b^{-1}a \in H
aH = {ah | h \in H} = class of a mod H
Notation: G/H = {gH | g\in G} = set of all cosets of H
|G/H| = [G:H] = |G|/|H|
Example: G = {e,a,b,c} Klein 4
H = < a> = {e,a}
|G| = 4
|H| = 2
[G:H] = |G|/|H| = 4/2 = 2
eH = H = {e,a} = aH
bH = {b,c} = cH
G/H = {eH, bH}
Example: G, H = G
[G:G] = 1
eG = G
G/G = {eG}
Example: G, H = {e}
[G:{e}] = |G|/1 = |G|
g{e} = {g}
G/{e} = {{g}| g\in G}
[Z:4Z] = 4
4Z = {0, \pm 4, \pm 8, ...}
1+4Z = {1+4k | k \in Z}
2+4Z = {2+4k | k \in Z}
3+4Z = {3+4k | k \in Z}
Z/(4Z) = {0+4Z, 1+4Z,2+4Z,3+4Z}
*** see photos
Def: H \subseteq G is subgroup is normal if \forall n \in H
and \forall g \in G, ghg^{-1} \in H
So H is closed under conjugation
Shorthand: gHg^{-1} \subseteq H
*** see photos
Example for normal subgroups:
1) {E} is a normal subgroup of G
2) G is a normal subgroup of G
Prop: Let \phi:G \rightarrow H be a homomorphism, then
ker \phi is a normal subgroup of G.
Proof: We already know ker \phi is a subgroup
Let x \in Ker \phi and g \in G
Want gxg^{-1} \in ker \phi
Check \phi(gxg^{-1}) = \phi(g) \phi(x) \phi(g^{-1}) = \phi(g)e\phi(g)^{-1}
Since x \in Ker \phi
So, gxg^{-1} \in Ker \phi
Therefore, Ker \phi is normal.
QED
What if we had done things differently and said
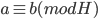if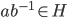 
This would work, but give a slightly different answer
This is an equivalence relation on G
All classes have size |H|,
that means [G:H] = # classes
- The class of g would be
Hg = {hg | h \in H}, right coset
Theorem: Let H be subgroup of G
the following are equivalent:
1) gH = Hg, for all g \in G
2) gHg^{-1} = H, for all g \in G, gHg^{-1}={ghg^{-1}|h \in H}
3) H is normal (gHg^{-1} subgroup of H
Proof:
1).=> 2): Assume gH = Hg
We want gHg^{1} = H
Let x \in gHg^{-1}. So x = ghg^{-1} with h \in H
Since gh \in gH = Hg
=> gh = h_1g for some h_1 \in H
So x = ghg^{-1} = h_1gg^{-1} = h_1 \in H
So x \in H_1 so gHg^{-1} \subseteq H
Let h \in H, Want h \in gHg^{-1}
hg \in Hg = gH so hg = gh_0, for h_0 \in H
Then h = gh_0g^{-1} \in gHg^{-1}
So, H \subseteq gHg^{-1}
H = gHg^{-1}
QED
2)=>3): gHg^{-1} = H implies gHg^{-1} \subseteq H "duh".
3) => 1): (circular reasoning?)
let g \in G
Want gH = Hg
step 1: Want gH \subseteq Hg
let x \in gH, so x = gh with h \in H
x = gh = ghg^{-1}g \in Hg since H normal => ghg^{-1} \in H
So gH \subseteq Hg
let z \in Hg, want z \in gH
So z = hg with h \in H
So z = gg^{-1}hg, this is conjugation = gg^{-1}h(g^{-1})^{-1} \in gH
since g^{-1}h(g^{-1}^{-1} \in H
because H is normal
so, Hg \subseteq gH, so gH = Hg
QED
Example: GL(2,R), all invertible 2x2 matrices
SL(2,R), all 2x2 matrices with det = 1
SL(2,R) is normal subgroup of GL(2,R).
If A, B \in SL(2,R)
det(BAB^{-1}) = det(B)det(A) 1/det(B) = det(A) = 1
So, BAB^{-1} \in SL(2,R) so SL(2,R) is normal.
det: GL(2,R) -> R-{0} with mult.
is a homomorphism
SL(2,R) = ker det
so its a normal subgroup
05/02/2016
Recap:
theorem 4.20
Today:
Quotient groups
If H \subseteq G is a normal subgroup, then G/H can be made a group by defining [x][y] = [xy]
Theorem: G/H with this "binary operation" is a group
Proof:
Need Mult. is
a function G/H X G/H -> G/H
Worry: Suppose [x]=[x'], [y]=[y']
[x][y] = [xy]
[x'][y'] = [x'y']
But ([x],[y]) = ([x'],[y'])
To be a function G/H X G/H -> G/H
need [xy] = [x'y']
Need x \equiv x' (mod H), y \equiv y' (mod H)
want xy \equiv x'y' (mod H)
Hey!!, the substitution principle gives this.
So [xy] = [x'y']
So the rule [x][y] = [xy]
is a legit bineary operation.
Check
Assoc:
[a]([b][c]) = [a][bc] = [a(bc)] = [(ab)c] by assoc in G. = [ab][c] = ([a][b])[c]
Identity:
Let e_G = identity of G
claim: [e_G] is identity for G/H
[e_G][a] = [e_G a] = [a] since e_G a = a
[a][e_G] = [a e_G] = [a]
So [e_G] is an identity for G/H
Inverses: If [a] \in G/H
theorem [a]^{-1} = [a^{-1}]
check: [a^{-1}][a] = [a^{-1}a] = [e_G]
[a][a^{-1}] = [aa^{-1}] = [e_G]
So [a^{-1}] = [a]^{-1}
So G/H is a group, done
Textbook says need to check closure in group, but prof. says no need since the definition of the binary operation requires closure. But this check is required for subgroup.
Change of notation:
We like to write gH instead of [g]
xH * yH = xyH, Product
e_G H = H, Identity
(aH)^{-1} = a^{-1}H, Inverse
Example: G = Z,+
H nZ where n >= 2
= < n >
= {nk | k \in Z}
G/H = \frac{Z}{nZ} = {m+nZ | m \in Z}
(m + nZ) + (k + nZ) = m+k + nZ
[m]+[k] = [m + k]
\frac{Z}{nZ} = Zn
Example: G = Z_6, +
H = <[3]> = {[0],[3]}
[G:H] = # cosets = |G|/|H| = 6/2 = 3
[0] + H = {[0],[3]}
[1] + H = {[1],[4]}
[2] + H = {[2],[5]}
H is a normal subgroup, since G is abelian.
So G/H is a group
(a + H) + (b + H) = (a+b)+H
Use table of [x]+H X [x]+H to show G/H is isomorphic to Z_3, +
The group of Quaternions,
Q = {1, -1, i, -i, j, -j, k, -k}
ij = k, jk = i, ki = j,
ji= -k, kj = -i, ik = -j
i^2 = j^2 = k^2 = -1
Q is a non-abelian group of order 8.
It has 6 elements of order 4. (i,j,k,-i,-j,-k), why not 3 elements?
Z[Q] = {1,-1}
Z[Q] is a normal subgroup of Q
# of cosets [Q:Z[Q]] = |Q|/|Z(Q)| = 8/2 = 4
1*Z(Q) = {1,-1}
iZ(Q) = {i,-i}
jZ(Q) = {j,-j}
kZ(Q) = {k,-k}
Check isomorphism to: Klein 4, not Z_4,+
Theorem: If H is a normal subgroup of G, then
G/H is called the quotient group of G by H.
Expect in Final, show table of quotient group
===
Define \Pi : G -> G/H
\Pi(g) = gH
Theorem 4.25, prof added (2)
Prop: If H is a normal subgroup of G, then:
1) \Pi : G-> G/H
\Pi(g) = gH is an onto homomorphism
2) Ker \Pi = H
Pf: 1)
Hom: Need \Pi(a)\Pi(b) = \Pi(ab)
\Pi(a)\Pi(b) = aH*bH = abH = \Pi(ab)
So, |pi is a hom.
Onto: Let gH \in G/H
Then gH = \pi(g). So \Pi is onto.
2) Ker \Pi = {g \in G | \Pi(g) = eH}
Where e = id of G
= {g \in G | gH = eH}
gH = eH <=> g \equiv e (mod H)
<=> e^{-1}g \in H
<=> g \in H
So \Pi(g) = gH is eH <=> g \in H
So H = Ker \Pi. Done
Cor: H \subseteq G is a normal subgroup IFF H is the kernel o some homomorphism.
Example: G = D_4 = symmetries of a square, Dihedral group of order 8
Rotations at zero deg: we get identity, Id
counterclockwise 90 deg: (1,2,3,4)
180 deg: (1,3)(2,4)
Counterclock 270 deg = 90 deg clockwise: (1,4,3,2)
Reflections across
L_1 : (1,2)(3,4)
L_2: (1,4)(2,3)
L_3: (2,4)
L_4: (1,3)
D_4 = the above guys
|D_4| = 8
Not isomorphic to Klein 4.
Google Coxeter group for symmetries
H = <[1,3][2,4]>
|H| = 2
H = Z(D_4) = center
[D_4:H] = |D_4|/|H| = 8/2 = 4
D_4/H
H = {Id, (1,3)(2,4)}
(1,2,3,4) H = {(1,2,3,4),(1,4,3,2)}
(1,2)(3,4)H = {(1,2)(3,4),(1,4)(2,3)}
(2,4)H = {(2,4),(1,3)}
Build table of D_4/H
{H, (1,2,3,4)H, (1,2)(3,4)H, (2,4)H}
Isomorphic to Klein 4 once 3 H found in the diagonal.
05/04/2016
Homework 6 is due Wed May 10
4.2: 2
4.3: 26
4.4: 2b, 4a, 6b, 12, 28
4.5: 2, 26,28,34
Recap example:
G = Z,+, H = 3Z = <3>
\Pi: G-> G/H
\Pi(g) = gH
Z/(3Z) = {0+3Z,1+3Z, 2+3Z}
\Pi: Z-> Z/(3Z)
\Pi(m) = m3Z = ...
see last entry, &
see photos & recording
5. Rings
05/09/2016
Ring Theory
Recap:
Ring examples:
Z, Q, R, C, Z_n, Mn(R), evens
If R has an identity e for mult., called unity, then r \in R is invertible or a unit if \exists s \in R with rs = e = sr
The units form a group under ., called the group of units.
Example: Z: unity is 1; invertible elements: {1,-1}
Example: Q unity is 1, invertible: Q - {0}
Z_6 unity: [1]; inv.: {[m] | gcd(m,n)=1}
Z_9: unity: [1]; inv.: {[1],[2],[4],[5],[7],[8]}
Mn(R): unity: e; inv. Gl(n,R) = {A\in Mn(R) | det(A) != 0}
Basic Properties of Ring:
1. 0 is unique
2. -x is unique
3. -(-x) = x
4. -(x+y) = -x + -y
5. a+x = a+y => x=y
Def: a \in R with a !=0 is called a zero divisor if ab = 0 with b != 0 in R.
when is [m] in Z_n a zero divisor?
when gcd(m,n) != 1
Why? let d = gcd(m,n) != 1
m = dk; n = dc
with k, l \in Z
k != m
c != n
mc = dkc = dck = nk = 0(mod n)
So, [m][c] = [0]
Since 1 \leq n < n, [c] != [0]
So [m] is a zero divisor in Z_n
Example: n = 12
m = 8
gcd(8,12) = 4
12 = 4*3
c=3; d=4
[8].[3] = [24] = [0]
5.2
Integral Domains & Fields
Def: A ring D is an integral domain if:
1. D is commutative
2. D has a unity e != 0
3. D has no zero divisors
Example: Z is an integral domain, so are Q, R, C.
Example: Even integers? No, no unity
Example: Z_4 is not an integral domain. [2] is a zero divisor
Example: Z_5 is an integral domain.
Example: Z_n is an integral domain IFF n is prime.
Because [m] is a zero divisor IFF gcd(m.n) != 1 for 1 \leq m < n
Theorem (Cancellation law) If D is in integral domain and a != 0 then ab = ac => b=c.
Pf: Assume ab = ac
thm ab-ac = 0
thm a(b-c) = 0
Since a != 0 => a is not a zero divisor => b-c = 0, so b=c.
Done.
Def: Let F be a ring, then F is a field.
1. F is commutative
2. F-{0} is a group under mult. (so F has a unity and all non-zero elements are invertible).
Example: R, Q, C, Z_2, Z_3, Z_n IFF n = prime.
Z is an integral domain but not a field.
Every field is an integral domain.
Pf: F is comm with unity by definition.
Check no zero divisors.
If a != 0 and ab = 0, want b = 0
then b = a^{-1}ab = a^{-1}.0 = 0
So a is not a zero divisor.
Prop: Every finite integral domain is a field.
5.3 Field of Quotients:
Rough idea: The construction of Q from Z by fractions can be made to work for any integral domain.
Example: Z[\sqrt{2}] = {a+b\sqrt{2} | a, b \in Z}
is a subring of R.
It is an integral domain but not a field.
Example: Gaussian integers
Z[i] = {a+bi | a,b \in Z} \subseteq Q
This an integral domain, not a field.
Now we extend an integral domain to a field using fractions.
1/2 => (1,2)
2/4 => (2,4)
(1,2) != (2,4)
We need to view fractions as equivalence classes of ordered pairs.
a/b = c/d with b, d != 0
ad = bc
let D be an integral domain:
Let S = {(a,b) | a, b \in D, b != 0}
Define an equivalence relation (a,b) ~ (c,d) iff ad = bc
Prof's To do list:
1) Prove ~ is an equivalence relation.
2) Check d/1 = c/1 IFF d=c
3) Need to check operations work.
05/11/2016
Homework 7 is due Wed, May 18.
5.1: 2b, 3, 7c,d, 17, 31
5.2: 6bcde, 12, 14, 20b
5.3: 8
Fractions
Recap
D, integral domain:
1. Comm
2. Mult. Id.
3. ab = 0 => a = 0 or b = 0
F field:
1. Comm
2. Unity = mult. identity
3. F-{0} is a group under mult.
Upshot:
1. Field are integral domains
2. Subrings of fields are integral domains
Goal: Every integral domain, D, is a subring of a field.
Def: If R, R' are rings, an isomorphism \psi: R-> R' is a bijection s.t.:
i) \psi(a+b) = \psi(b) + \psi(b)
ii) \psi(ab) = \psi(a)\psi(b)
We say R is isomorphic to R'
Goal: Prove each integral domain D is isomorphic to a subring of a field.
Setup:
- D is an integral domain
- S = {(a,b) | a\in D, b\in D, b!= 0}, "potential fractions a/b".
Define an equivalence relation on S by
(a,b) ~ (c,d) if ad = bc (outer*outer = inner*inner)
Prop: ~ is an equivalence relation
Pf: Reflexive: (a,b)~(a,b) since ab = ba because D is commutative.
Symmetric: (a,b) ~ (c,d) want (c,d)~(a,b)
Given: ad = bc, want cb = da, but cb=da by comm.
Transitive: (a,b)~(c,d) and (c,d)~(x,y)
want: (a,b)~(x,y)
given: ad=bc, cy=dx
want ay=bx
Trick: ady = bcy = bdx
so d(ay) = d(bx) since d != 0
and integral domains have cancellation lan.
So ay = bx => (a,b)~(x,y)
So, ~ is an equivalence relation. Done
From now on the equiv. class of (a,b) \in S is written a/b. Then a/b = c/d <=> ad = bc
Note: \frac{ad}{bd} = a/b if d != 0.
Since abd = adb.
Addition and mult.
Multiplication:
For this to make good sense
Need if a/b = a'/b' and c/d = c'/d'
then \frac{ac}{bd} = \frac{a'c'}{b'd'}
Given ab' = a'b, cd' = dc'
So acb'd' = ab'cd' = a'bdc' = a'c'bd
So, \frac{ac}{bd} = \frac{a'c'}{b'd'}
So mult. makes sense.
Assoc:
(a/b \cdot c/d) \cdot x/y =^{def} \frac{ac}{bd} \cdot x/y
=^{def} \frac{(ac)x}{(bd)y} = \frac{a(cx)}{b(dy)} by assoc in y
=^{def} \frac{a}{b}\frac{cx}{dy} =^{def} \frac{a}{b}(\frac{c}{d}\cdot\frac{x}{y})
Comm:
(a/b)(c/d) =^{def} \frac{ac}{bd} = \frac{ca}{db} =^{def} \frac{c}{d}\cdot \frac{a}{b}
Since D is comm.
Mult. identity: If 1 is unity of D,
1/1 is the unity of Q = set of fractions
1/1 \cdot a/b = \frac{1\cdot a}{1\cdot b} = a/b
Addition:
a/b + c/d =^{def} \frac{ad+bc}{bd}
You can check:
a/b = a'/b' and c/d = c'/d' then
\frac{ad+bc}{bd} = \frac{a'd'+b'c'}{b'd'}
Assoc:
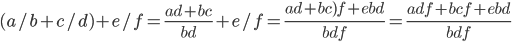
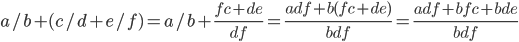
So + is assoc.
Additive identity:
0/1 => a/b + 0/1 = \frac{a+0\cdot b}{b} = a/b
Comm:
a/b + c/d = \frac{ad+bc}{bd} = \frac{bc+ad}{db} = c/d + a/b
Additive inverse:
-(a/b) = -a/b since a/b + -a/b = \frac{ab-ab}/b^2 = 0/b^2 = 0/1
Distributive law:
a/b(c/d + e/f) = a/b(\frac{cf+de}{df}) = \frac{acf+ade}{bdf}
a/b \cdot c/d + a/b \cdot e/f = \frac{ac}{bd} + \frac{ae}{bf} = \frac{acbf+aebd}{b^2df}
=b/b \cdot \frac{acf+aed}{bdf} = \frac{acf+aed}{bdf}, since b/b = 1/1
Mult. inverses for non-zero guys
If a/b != 0/1
then a.1 != b.0 = 0
So a/b != 0/1 iff a != 0
Mult. inverse of a/b if a != 0 is b/a
Check a/b \cdot b/a = \frac{ab}{ab} = 1/1
So, Q is a field.
We wanted D is isomorphic to a subring of Q
Define \phi: D-> Q, by \phi(d) = d/1
Let D'= {d/1 \in Q | d\in D}
D' is a subring containing the unity 1/1.
- has 0/1
- Closed under +: d/1 + d'/1 = \frac{d+d'}{1} \in D'
- closed under .: d/1 . d'/1 = dd'/1 \in D
- closed under -: -(d/1) = (-d)/1 \in D'
So \phi: D-> D', \pshi(d) = d/1
Iso:
1. \phi(d_1 + d_2) = \frac{d_1 + d_2}{1} = d_1/1 + d_2/1 = \phi(d_1)+\phi(d_2)
2. \phi(d_1d_2) = d_1d_2/1 = d_1/1 . d_2/1 = \phi(d_1)\cdot \phi(d_2)
\phi: D-> D' is a bijection:
If x \in D' => x = d/1 with
d\in D. So x = \phi(d)
So e is onto.
If \phi(d_1) = \phi(d_2)
want d_1 = d_2
d_1/1 = \phi(d_1) = \phi(d_2) = d_2/1
So d_1/1 = d_2/1 => 1.d_1 = d_2.1, so d_1 = d_2. So \phi is injective.
Thus, \phi is an isomorphism.
Done
Chapter 8
8.1 Polynomials over a ring.
The point of modern algebra in history => solve polynomial roots.
Let R be a comm. ring with unity 1.
Let x be an indeterminate.
Then a polynomial over R is an expression of the form
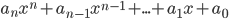
with n \geq 0 and a_0,...,a_n \in R
Two poly are equal if their coefficients are the same with the proviso (warning) 0+3x+0x^2 = 3x etc.
The set of all poly over R is denoted R[x]
Example: [3]x^2 + [2]x + [1] \in Z_4[x]
Example: [2]_4 x in Z_4[x]
What are the roots?
x = [0]_4, [2]_4
Notice two roots for a degree are polynomial.
In \sum -notation we can write polynomials as
addition & multiplication of polynomials
These formulas do what you think
([2]x+[1])([2]x^2 + [3]x) in Z_4[x]
= [3]x + [2][3]x^2 + [1][2]x^2 + [2][2]x^3
= [3]x + ([2]+[2])x^2 = [3]x
In High School:
deg(f(x)g(x)) = deg f(x) + deg g(x)
Where degree f(x) = n if x^n is the highest power in f(x) with a non-zero coefficient.
This didn't work in Z_4[x]
Prop: If R is a comm. ring with unity, then R[x] is a comm. ring with unity.
The zero is the zero polynomial and the unity is the constant polynomial 1.
We don't define the degree of the zero polynomial.
Prop: Let D be an integral domain, then D[x] is an integral domain.
Moreover deg (f(x)g(x)) = deg (f(x)) + deg (g(x))
Pf: Let f(x) = a_0+a_1x + ... + a_nx^n with an != 0 has degree n.
let g(x) = b_0 + b_1x + ... + b_mx^m with b_m != 0 have degree m.
f(x)g(x) = a_nb_m x^{n+m} + lower order terms
Since a_n != 0, b_m != 0 and D is an integral domain => a_nb_m != 0.
So f(x)g(x) != 0 and deg(f(x)g(x)) = n + m = deg(f) + deg(g). Done
We can now do fractions with D[x].
Example: \mathbb{Z}[x]
Fractions e.g. \frac{2x^2+3}{x^3+x-4}
05/16/2016
Chapter 8
Last time: R ring
R(x) = all polynomials in indeterminante x with coefficients in R
Last time: R integral domain =>
R[x] is an integral domain
In this case deg(f(x)g(x)) = deg(f(x)) + deg(g(x))
F a field
Def:
A Polynomial f(x) \in F[x]
is monic if its leading coefficient is 1.
Example: x^2 + 2x - 1, is monic in Q[x]
3x^3 + 2x + 1 is not monic
Theorem (Division algorithm)
let F be a field
and f(x), g(x) \in F[x]
with f(X) != 0 then there exist unique q(x) and r(x) \in F[x] with
g(x) = q(x) + f(x) + r(x)
and either r(x) = 0 or deg r(X) < deg(fx)
q(x) => quotient
r(x) => remainder
Example: F = Q
f(x) = x^2 + 1
g(x) = 3x^4 - 2x^3 + 4x^2 -3x + 2
write g(x) = q(x)f(x) + r(x)
r(x) = 0 or deg r(x) < deg f(x)
do g(x)/f(x)
3x^4 -2x^3 + 4x^2 -3x+2 = (3x^2-2x+1)(x^2+1)+(-x+1) = q(x)(x^2+1) + r(x)
Example: F = Z_3
f(x) = [2]x^2 + [1]
g(x) = [1]x^3 + [2]x + [1]
write g(x) = q(x)f(x) + r(x) with r(x) = 0 or deg r(x) < deg(f(x))
do g(x)/f(x)
we get [2]x([2]x^2 + [1]) + [1] = q(x)([2]x^2+[1]) + r(x)
Def: If f(x), g(x) \in F(x) are polynomials over a field F, not both zero, then d(x) \in F(x) is a gcd of f(x) and g(x) if:
1) d(x) | f(x) and d(x) | g(x)
2) if h(x) | f(x) and h(x) | g(x), then h(X) | d(x)
3) d(x) is monic (leading coeff. is 1)
---
Reminder: d(x) | f(x) if f(x) = d(x) c(x) for some c(x) \in F(x)
---
Example: gcd(x^-1, x^3-1) in Q[x] = x-1
x^2-1 = (x-1)(x+1)
x^3-1 = (x-1)(x^2+x+1)
Thm: Let F be a field and f(x), g(x) \in F(x) not both 0. Then f(x) and g(x) have a unique gcd. Moreover gcd(f(x),g(x)) is the smallest degree polynomial d(x) s.t.
d(x) = a(x)f(x) + b(x)g(x) for some a(x), b(x) \in F(x).
Pf: Same as for integers.
We can compute d(x), a(x), b(x) using Euclidian algorithm
Example:
Find gcd of x^4 - 1 and x^3+2x^2+x+2 in Q[x]
step 1: do (x^4-1)/(x^3+2x^2+x+2) = (x-2)(...)+(3x^2+3)
The the left:
x^3+2x^2+x+2 = 3(x^2+1)... => 3(x^2+1)(x/3 + 2/3) + 0
do (x^3+2x^2+x+2)/(3x^2+1)
gcd(x^4-1,x^3+2x^2 + x+ 2) = x^2+1
Note: You must multiply the last remainder by 1/leading coeff. to get monic.
example: gcd(x^3 + x + 1, x^2+2x+1) in Q[x]
x^3+x+1 = (x^2+2x+1)(x-2) + 4x+3
x^2+2x+1 = (4x+3)(x/4+5/16)+16
4x+3 = 1/16(64x+48) + 0
gcd(x^3+x+1,x^2+2x+1) = 1
since the monic version of 1/16 is 1
Example: gcd(x^2-1,x^3-1) = x-1
Def: If f(x) is a polynomial with coefficients in a ring R, then r \in R is a root of f(x) if f(x) = 0
Rational roots test:
Thm: Let p(x) = a_0 + a_1x+...+a_nx^n \in Z[x]
with a_n != 0, n \geq 1
If r/s \in Q is a root with gcd(r,s) = 1
then s|a_n, r|a_0
Example: f(x) = 2x^4 - 1
Does this have a rational root?
r/s
r|-1
s|2
r = \pm 1
s = \pm 1, \pm 2
f(1) = 2-1 = 1
f(-1) = 2-1 = 1
f(1/2) = 1/8 - 1 = -7/8
f(-1/2) = -7/8
So no rational roots.
Cor: If n \in Z is not a perfect square, then \sqrt{n} is irrational.
Pf: f(X) = x^2 - n
Apply rational roots test
If r/s is a root in lowest terms
r|-n
s|1 => s = \pm 1
So any rational root must be an integer.
r/s = \pm r. If 0 = f(r) = r^2 - n with r \in Z => n = r^2
So n is a perfect square.
So if n is not a perfect square x^2 - n has no rational root so \sqrt{n} is irrational.
Cor: If f(x) = x^n + a_{n-1}x^{n-1}+...+ a_0 is a monic polynomial with integer coeffs, then each rational root of f(x) is an integer.
Pf: denominator of rat root r/s divides 1 by rational roots test.
----
Proof of rats root test:
Let r/s \in Q be a root of f(x) = a_0 + a_1x+...+a_nx^n with a_n != 0, n \geq 1 and f(x) \in Z[x]
Assume gcd(r,s) = 1
0=f(r/s) = a_0+a_1r/s + a_2(r^2/s^2) + ... + a_n(r^n/s^n)
step 1: clear denominators multiply both sides by s^n.
O = a_0s^n + a_1rs^{n-1} + a_2r^2s^{n-2} + ... + a_nr^n
=> a_0s^n = -(a_1rs^{n-1}+...+a_nr^n} = -r(....)
so r | a_0s^n
Since gcd(r,s) = 1 => r | a_0
Similarly a_nr^n = -(...) = -s(...)
So s|a_nr^n
since gcd(s,r) = 1 => s | a_n. Done.
Prop: Let f(x) \in F[x] with F a field
Then \alpha \in F is a root of f(x) IFF x - \alpha divides f(x)
Proof: If x-\alpha | f(x) => f(x) = g(x)(x-\alpha) for some g(x)+F[x]
So f(\alpha) = g(\alpha)(\alpha-\alpha) = 0
Suppose \alpha is a root of f(x). Want x-\alpha | f(x)
Write using division algorithm
f(x) = q(x)(x-\alpha) + r(X) where r(x) = 0 or deg r(x) < deg (x-\alpha) = 1
So r(x) = 0 or deg r(x) = 0
Either way r(x) is a constant polynomial c \in F
So f(x) = q(x)(x-\alpha) + c
Plug in x = \alpha
Since \alpha is a root of f
0= f(\alpha) = q(\alpha)(\alpha - \alpha) + c = c
so, c = 0;
So f(x) = q(x)(x-\alpha) . Done
So x-\alpha | f(x)
Cor: If F is a field and f(x) \in F[x] has degree n \leq 1, then f(X) has at most n distinct roots in F.
Example: [2]x = 0 in Z_4[x]
has 2 roots x=[0],[2]. Note Z_4 is not a field
Pf: By induction n
Base case: n = 1
f(x) = mx + b; m,b \in F, m != 0
If r is a root
0 = f(r) = mr + b
So r = -b/m
Assume true for n, prove for n+1.
Let f(x) \in F[x] have degree n+1
Easy case: f(x) has no roots in F.
Then # of roots of f(x) in F is 0 \leq n+1. Done in this case
Assume f(x) has a root a \in F.
Then f(x) = g(x)(x-a) by the above.
Since F is a field, deg f(x) = deg g(x) + 1, so deg g(x) = deg f(x) -1 = n+1-1 = n
So by induction g(x) has at most n roots.
If b is a root of f(x), then
0 = f(b) = g(b)(b-a)
since g(b), b-a \in F and F has no zero divisors => b=a or g(b) = 0
So roots of f(x) = roots of g(x) U {b}
=> f(x) has at most n+1 distinct roots. Done.
Def: If F is a field a polynomial f(x) \in F[x] is irreducible if
1) f(x) is not a constant
2) f(x) = g(x)h(x)
with g(x), h(x) \in F[x]
then g(x) or h(x) is a constant
Example: f(x) = mx + b with m != 0, then f(x) is irreducible.
Prop: If f(x) has degree 2 or 3 then f(x) is irreducible IFF it has no root.
Proof: If f(x) = g(x)h(x) with neither g(x) nor h(x) a constant, then
2 or 3 = deg f(x) = deg g(x) + deg h(x)
since deg f(x), deg g(x) > d or 0?
so deg g(x) = 1 or deg h(x) = 1 or both
but a degree one polynomial mx+b has root -b/m.
So if f(x) can be factored it has a root.
On the other hand if f(x) has a root \alpha then x-\alpha divides f(x) so f(x) is not irreducible.